Problema 232
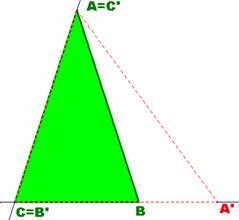
Sea ABC un triángulo isósceles siendo AB = AC . Hallar x real tal que si tomamos a + x , b + x , c + x , prolongando una longitud x a a desde B , y obteniendo C' , prolongando una longitud x a b desde C y obteniendo A' , y prolongando una longitud x a c desde A y obteniendo B' , el triángulo A'B'C' sea isósceles, siendo B'C' = B'A' .

Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid. Romero, J.B. (2005): Comunicación personal.
Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Solución:

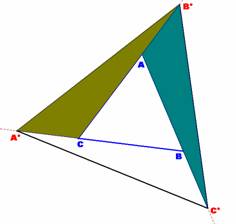
Sea el triángulo isósceles ABC, de lados iguales AC = AB = p. Sea x la longitud que le añadimos, siguiendo las instrucciones del enunciado. En definitiva, BC’ = CA’ = AB’ = x. Si queremos que el triángulo así construido A’B’C’ sea isósceles con B'C' = B'A' , como lados iguales, tendrán que verificarse las siguientes igualdades:

A’B’² = x² + (p+x)² −2∙x∙(p+x)∙cos[(p+A)/2]; B’C’² = x² + (p+x)² −2∙x∙(p+x)∙cos(p−A)
De estas relaciones, deducimos que:

Caso 1.- x = −p

En este caso sucederá entonces que: A’B’² = B’C² = p² ;

Así el triángulo A’B’C’ será también isósceles.

Caso 2.- x ≠ −p

Dividimos por el factor (x+p) y obtenemos que: cos[(p+A)/2] = cos(p−A),

Desarrollando esta ecuación trigonométrica:

cuya única solución válida será:
, es decir, .
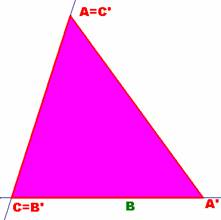
Esta respuesta significa que el triángulo isósceles inicial ABC ha de ser equilátero y así, de este modo, siempre sería válida la construcción para cualquier valor de x, siendo igualmente equilátero el triángulo A’B’C’ construido.