|
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid Problema 232 Sea ABC un triángulo isósceles siendo AB = AC . Hallar t real tal que si tomamos a + t , b + t , c + t , prolongando una longitud t a a desde B , y obteniendo C' , prolongando una longitud t a b desde C y obteniendo A' , y prolongando una longitud t a c desde A y obteniendo B' , el triángulo A'B'C' sea isósceles, siendo B'C' = B'A'. Romero, J.B. (2005): Comunicación personal. Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de abril de 2005) |
| INTRODUCCION - DISCUSION |
Vamos pues a realizar una solución de lo más general, no posible con regla y compás; pero si con CABRI II Plus. Para ello y siguiendo el enunciado, utilizaremos un parámetro real t cualquiera y obtendremos nuestros puntos en función de t: Determinaremos ahora un punto B”(t) que con los dos anteriores cumpla con el enunciado; pero relajando una de las condiciones. Nosotros relajamos la condición de que B”(t) esté sobre AB Imponemos ahora la primera condición relacionada con la formación del triángulo isósceles que exige que B”(t) esté sobre la mediatriz de A”(t) y C”(t) Imponemos también la segunda condición que nos dice que B”(t) está a distancia t de A (círculo de centro A y radio t) Por lo tanto el lugar geométrico de las posiciones de B”(t) es la siguiente intersección Reintroduciendo ahora la condición relajada más arriba tenemos la solución B’ para el valor del parámetro ts El triángulo A’B’C’ es la solución buscada. Utilizaremos la herramienta lugar geométrico y la intersección de lugares geométricos con otros objetos, ambas disponibles en CABRI II Plus. Con todas las combinaciones posibles de signos, se obtienen seis soluciones, dos de ellas triviales (t=0). No se obtienen soluciones para t>0. |
| SOLUCION |
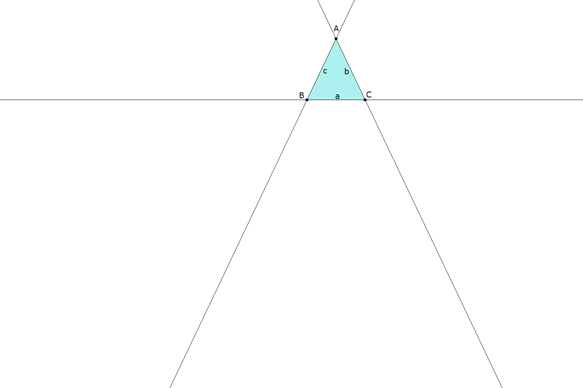 figura 1 Dibujamos el enunciado A,B,C. |
| DEFINICION DEL PARAMETRO t |
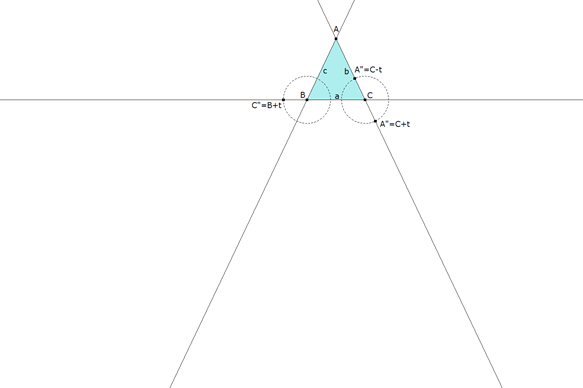 figura 2 Sobre BC y tal como se aprecia en la figura, definimos un parámetro t de acuerdo al enunciado. (Punto sobre un objeto) Al mismo tiempo trazamos ΓB(t), el círculo de centro en B y radio t. (Círculo) También trazamos ΓC(t), el círculo de centro en C y radio t. (Círculo) |
| CASO [A”(t)=C-t] - MEDIATRIZ DE A”(t) y C”(t) - CIRCULO ΓA(t) - B”(t) |
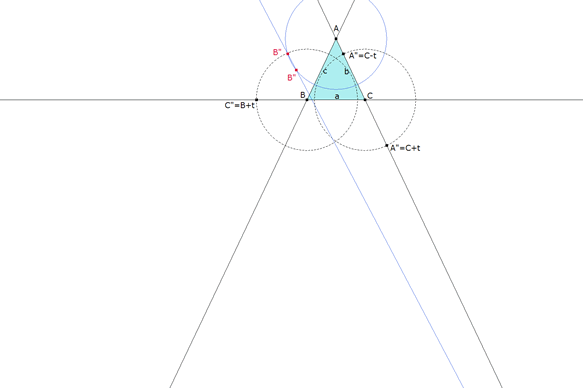 figura 3 Consideramos el caso A”(t)=C-t. ΓA(t). Con centro en A, círculo (azul) de radio t. (Compás) Mediatriz de C”(t)A”(t) (azul). (Mediatriz) Las dos intersecciones posibles entre círculo y mediatriz nos dan B”. (Punto(s) de intersección) |
| DETERMINACION DEL PRIMER LUGAR GEOMETRICO B”(t) |
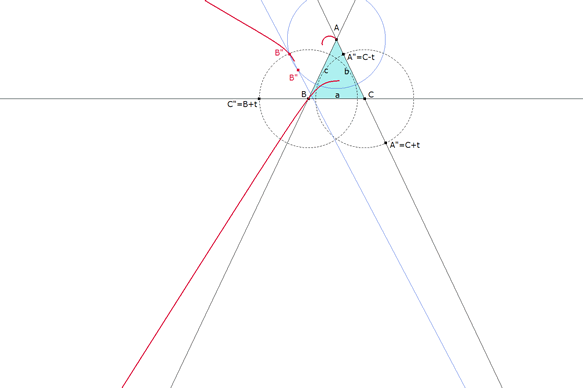 figura 4 Lugar geométrico de la primera intersección B” cuando se desplaza C” sobre BC. (Lugar) |
| DETERMINACION DEL SEGUNDO LUGAR GEOMETRICO B”(t) |
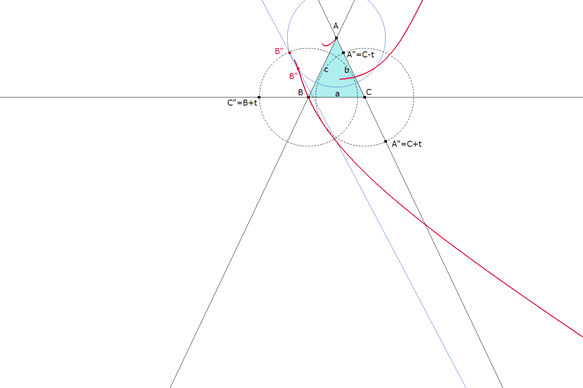 figura 5 Lugar geométrico de la segunda intersección B” cuando se desplaza C” sobre BC. (Lugar) |
| CASO [A”(t)=C+t] - MEDIATRIZ DE A”(t) y C”(t) - CIRCULO ΓA(t) - B”(t) |
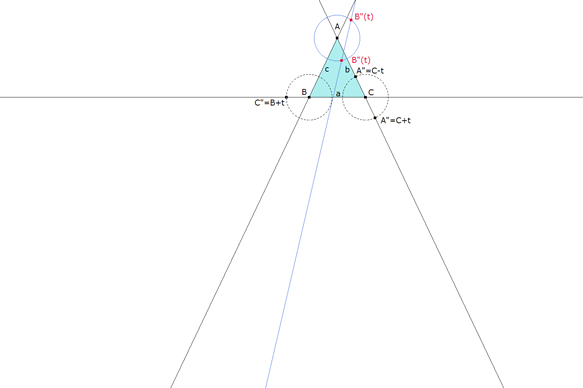 figura 6 Consideramos el caso A”(t)=C+t. ΓA(t). Con centro en A, círculo (azul) de radio t. (Compás) Mediatriz de C”(t)A”(t) (azul). (Mediatriz) Las dos intersecciones posibles entre círculo y mediatriz nos dan B”. (Punto(s) de intersección) |
| DETERMINACION DEL TERCER LUGAR GEOMETRICO B”(t) |
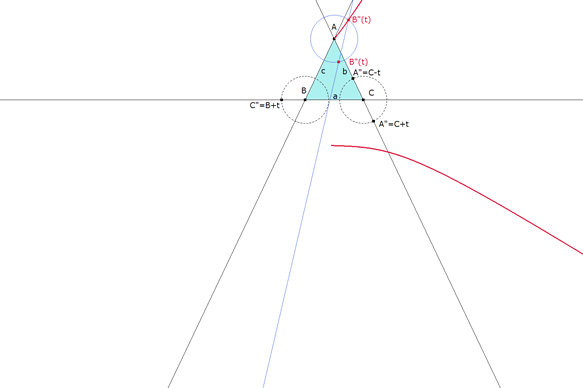 figura 7 Lugar geométrico de la tercera intersección B” cuando se desplaza C” sobre BC. (Lugar) |
| DETERMINACION DEL CUARTO LUGAR GEOMETRICO B”(t) |
 figura 8 Lugar geométrico de la cuarta intersección B” cuando se desplaza C” sobre BC. (Lugar) |
| DETERMINACION DEL LUGAR GEOMETRICO GENERAL B”(t) Y LAS SEIS SOLUCIONES |
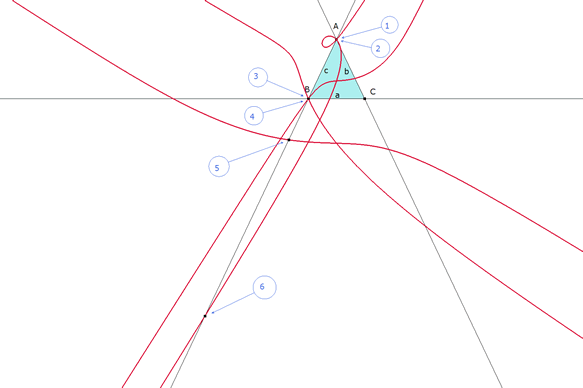 figura 9 La unión de los cuatro lugares determinados constituye un solo lugar que alberga todas las combinaciones de signos en la determinación de las soluciones. Este lugar presenta seis intersecciones numeradas del 1 al 6 entre el lugar y la recta AB. (Punto(s) de intersección) |
| SOLUCIONES 1 Y 2 |
Viendo la figura 9 observamos que en estas soluciones B” coincide con A dos veces; lo que significa que t=0. Estas dos soluciones son triviales y reproducen el triángulo ABC original. |
| SOLUCION 3 |
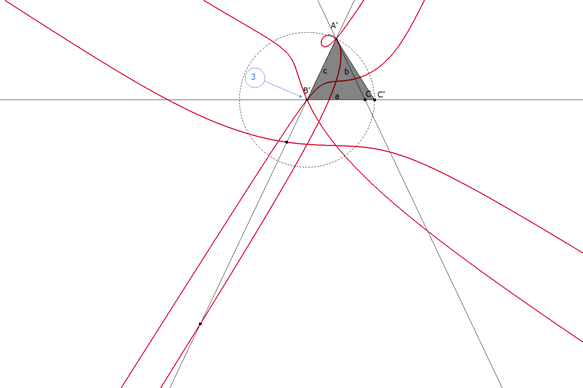 figura 10 En esta solución B’ coincide con B y por lo tanto t=-c. C’=B-c; A’=A=C-c. ESTA ES LA ÚNICA SOLUCIÓN QUE RESPONDE EXACTAMENTE AL ENUNCIADO. |
| SOLUCION 4 |
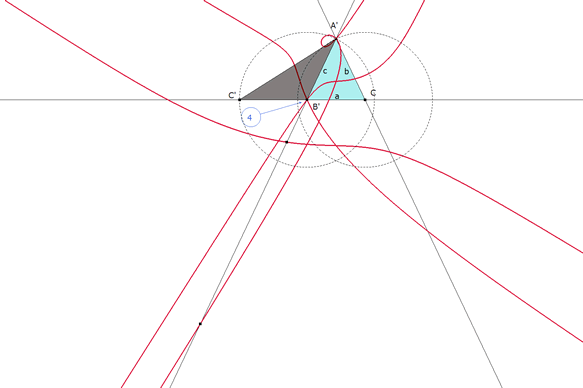 figura 11 En esta solución B’ coincide con B y por lo tanto t=-c. C’=B+c; A’=A=C-c. |
| SOLUCION 5 |
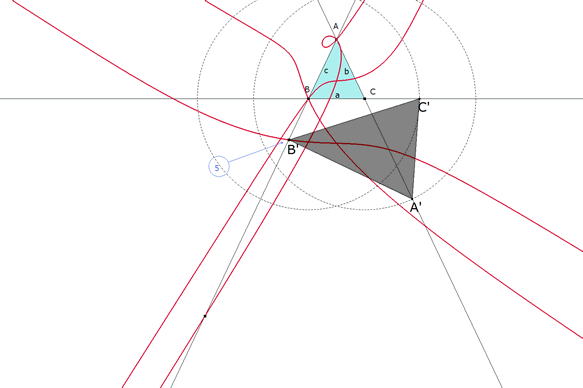 figura 12 En esta solución ts<0. B’=A+ts; C’=B+ts; A’=A=C-ts. |
| SOLUCION 6 |
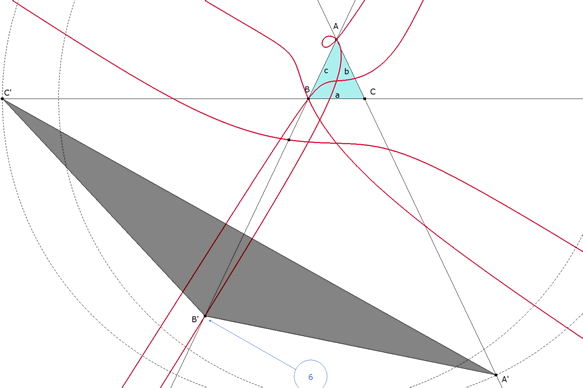 figura 13 En esta solución también ts<0. B’=A+ts; C’=B-ts; A’=A=C-ts. |