Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 232
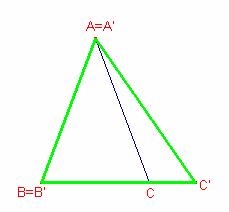
Sea ABC un triángulo isósceles siendo AB = AC . Hallar x real tal que si tomamos a + x , b + x , c + x , prolongando una longitud x a a desde B , y obteniendo C' , prolongando una longitud x a b desde C y obteniendo A' , y prolongando una longitud x a c desde A y obteniendo B' , el triángulo A'B'C' sea isósceles, siendo B'C' = B'A' .
Romero, J.B. (2005): Comunicación personal.
 Solución deRicard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València) (1 de octubre de 2004) (en español) :
Solución deRicard Peiró i Estruch Profesor de Matemáti cas del IES 1 de Xest (València) (1 de octubre de 2004) (en español) :
Sea el triángulo isósceles ![]() ,
, ![]() .
.
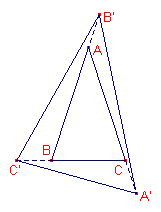
Sea ![]() .
.
Sea ![]()
Notemos que ![]() ,
, ![]() .
.
Aplicando el teorema del coseno ![]() :
:
![]() .
.
Aplicando el teorema del coseno al triángulo ![]() :
:
![]() .
.
Para que el triángulo ![]() sea isósceles
sea isósceles ![]() :
:
![]() Simplificando:
Simplificando:
![]() .
.
Las soluciones son:
![]() , solución trivial.
, solución trivial.
![]() ,
, ![]() ., en este caso cualquier real positivo x cumple que el triángulo
., en este caso cualquier real positivo x cumple que el triángulo ![]() sea isósceles
sea isósceles ![]() .
.
![]() .
.