Problema 233
Sea H el ortocentro del
triángulo acutángulo ABC y M el punto medio del lado BC.
Sea X el punto en que la recta HM interseca el arco BC (que no contiene a A) de
la circunferencia circunscrita a ABC.
Sea Y el punto de intersección de la recta BH con la
circunferencia distinto de B. Demostrar que XY = BC.
EUEKA 2, 1998, Sociedade Brasileira de Matemática (pag 229 ) http://www.obm.org.br/eureka/eureka2.pdf
Publicado con permiso de
Solución de F. Damián Aranda Ballesteros, profesor del
IES Blas Infante de Córdoba.
|
|
|
|
Solución:
De la figura realizada, observemos los siguientes hechos de
interés:
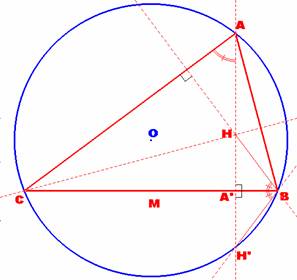
1) Si A’ es el pie de la altura relativa al vértice
A, H el ortocentro y H’ el punto donde la altura
corta a la circunferencia circunscrita, entonces tenemos que:
HA’ =A’H’.
Para ello, observamos que el ángulo
<CBH’ = <H’AB = <CBH. De este modo, los
triángulos rectángulos en A’, BA’H y
BA’H’ tiene además un ángulo igual y un cateto
común, el A’B.
Por lo tanto A’H =A’H’.
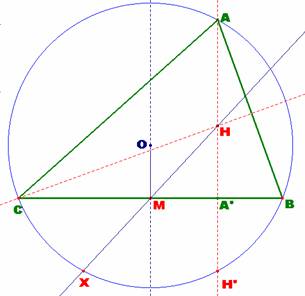
2) Por ser A’H = A’H’, si consideramos la
simetría de eje, el lado BC, ésta transforma el punto H en
H’. Si ahora razonamos con la simetría de eje, la mediatriz de BC,
resulta que el punto transformado de H’ debe coincidir necesariamente con
el simétrico de H respecto del punto M, y este punto no es otro
más que el punto X.
De esta hecho, obtenemos que el ángulo HH’X es recto.
Así también lo será, el ángulo AH’X, y por
tanto los puntos X y A serán diametralmente opuestos.
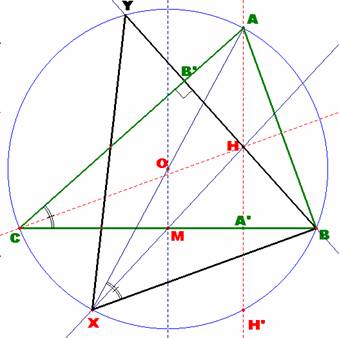
3) Probamos que BC = XY.
Como ambos segmentos son cuerdas de una misma circunferencia, veremos
que los arcos que subtienden son de igual medida.
|
|
Para ello, tenemos que el ángulo que subtiende la cuerda BC es
<A y que:
<A = <CAX + <XAB.
Y, por otro lado, el ángulo que subtiende la cuerda XY es
<XBY y que:
<XBY = <XBC + <CBY.
Como quiera que <CAX = <XBC, (=ambos subtienden la misma cuerda
CX), sólo falta probar la igualdad entre los otros dos sumandos.
Y esto es evidente sin más que considerar que: <XAB
= 90º − <AXB = 90º − <C
Por otra parte, también es verdad que: <CBY
=90º − <C.
De esta forma, ambos ángulos al estar inscritos en la misma circunferencia son
iguales y subtienden cuerdas de la misma longitud; BC = XY