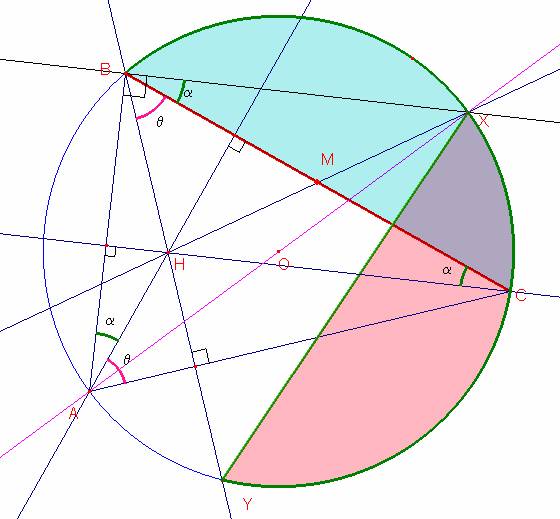
Problema 233
Sejam H o ortocentro (interseção das alturas) do triângulo acutângulo ABC e M o ponto médio do lado BC . Seja X o ponto em que a reta HM intersecta o arco BC (que não contém A ) da circunsferência circunscrita a ABC . Seja Y o ponto de interseção da reta BH com a circunsferência, distinto de B . Demonstre que XY = BC.
(Traducción del editor)
Sea H el ortocentro del triángulo acutángulo ABC y M el punto medio del lado BC.
Sea X el punto en que la recta HM interseca el arco BC (que no contiene a A) de la
Circunferencia circunscrita a ABC.
Sea Y el punto de intersección de la recta BH con la circunferencia distinto de B.
Demostrar que XY = BC.
EUEKA 2, 1998, Sociedade Brasileira de Matemática (pag 229 )
http://www.obm.org.br/eureka/eureka2.pdf
Publicado con permiso de
Solución del Prof. William Rodríguez Chamache:
Para demostrar que las cuerdas BC y XY son congruentes demostraremos que: <BXC=<XCY
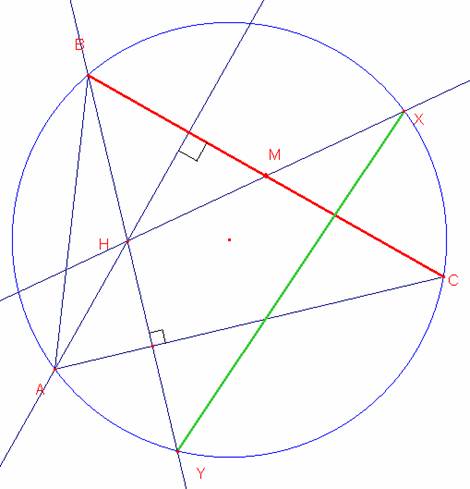
Por propiedad sabemos que El simétrico del punto H (ortocentro) con respecto al punto M (punto medio de BC) es el punto X que pertenece a la circunferencia circunscrita al triángulo también sabemos que los puntos A, O y X son colineales siendo O el circuncentro del triángulo ABC.
La demostración de estas propiedades las encuentras en: www.geometriainteractiva\hallasgos\demos2.htm
En el gráfico AOX es el diámetro
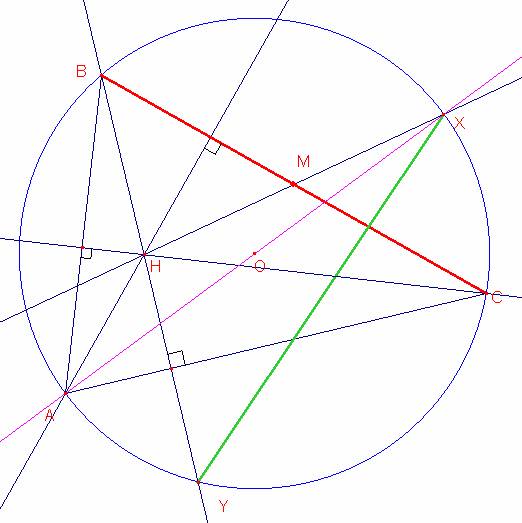
Luego el triángulo ABX es rectángulo en B, Ahora las rectas que contienen BX y HC son paralelas
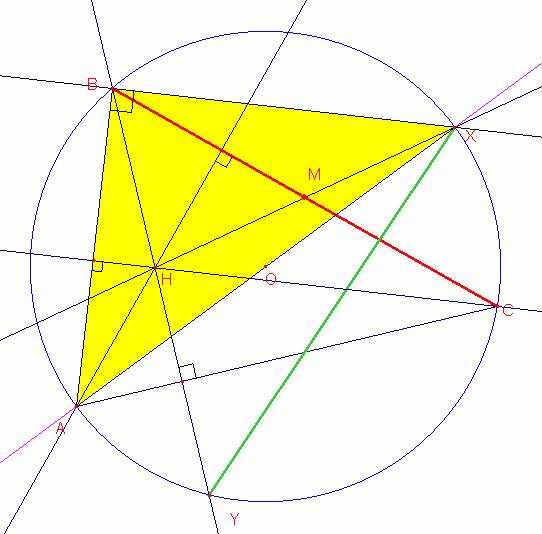
Del grafico observamos que los ángulos <HAC=<HBC=θ pero <YOC=2θ
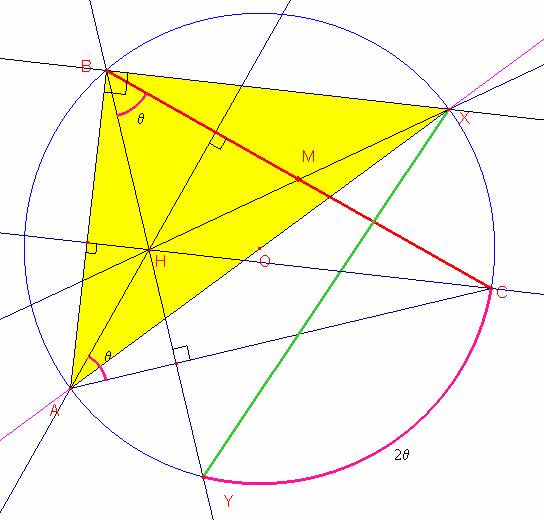
También observamos que los <XBC=<BCH=<HAB=α y la medida de <COX=2 α
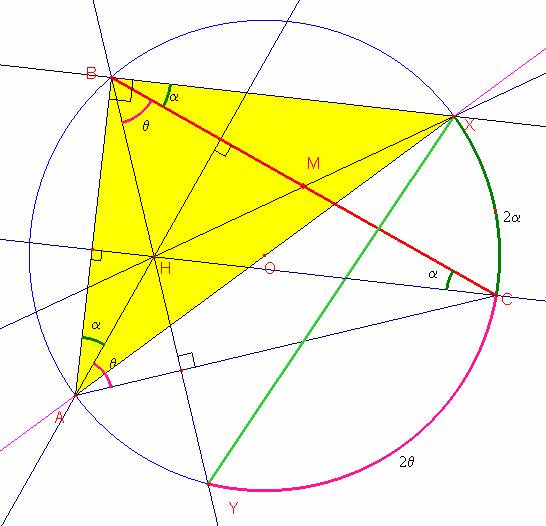
Finalmente observamos que los arcos BXC y XCY son iguales a 2θ+2α por lo tanto las cuerdas BC y XY son iguales.