Problema 234

Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia.

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría"
Ed . Mir . Pàgina 31. (50)
Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Solución:

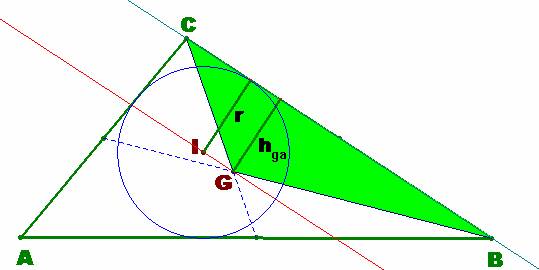
Sea el triángulo ABC, de lados a, b= a−x y c= a+x.

1) Si este triángulo tiene de área S, el radio de la circunferencia inscrita, r = inradio, verificará que p∙r = S, siendo p igual al semiperímetro.
De esta manera, .

2) Si ahora consideramos el área del triángulo GBC, determinado por el vértice G, baricentro del triángulo ABC, tenemos que:

Area(GBC)= 1/3∙S

Por otra parte,

Area(GBC)= 1/2∙a∙h_ga

Donde h_ga representa la distancia de G al lado BC.

En definitiva,

3) Si calculamos p, obtenemos que: 2∙p = a + (a−x) + (a+x) =3∙a;

4) En definitiva, deducimos la igualdad siguiente: r = h_ga
Este hecho indica que los puntos I (incentro) y G (baricentro) distan lo mismo del lado a, luego están situados en una recta paralela al lado de longitud intermedia entre los lados de un triángulo que forman una progresión aritmética, c.q.d.