Problema 234 de triánguloscabri |
|
Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia. |
|
Gúsiev, V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" .Propuesto por Ricard Peiró i Estruch |
Solución de Francisco Javier García Capitán
Este es un problema que se resuelve de una forma rápida con coordenadas baricéntricas, siendo los cálculos los suficientemente sencillos como para servir también de introducción al uso de estas coordenadas.
Podemos suponer, sin pérdida de generalidad que es
El baricentro G y el incentro I del triángulo ABC tienen coordenadas baricéntricas G = (1, 1, 1) e I = (a, b, c), respectivamente. Entonces, la ecuación de la recta GI es
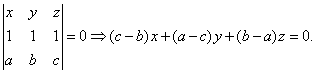
La intersección de GI con la recta AC (de ecuación
) es el
punto 
.
Si los lados del triángulo están en progresión aritmética
será 
por lo que las coordenadas de P suman 0 y P es un punto del
infinito. Al cortarse el lado AC y la recta GI en un punto
del infinito, ambas rectas son paralelas.
Para obtener
una figura con Cabri de los triángulos que satisfacen las condiciones
del problema fijamos el segmento de longitud BC = a, y consideramos
un punto variable N en BC. Interpretando que BN=c
y teniendo en cuenta la relación
hallamos el simétrico N' de N respecto de B
y el punto medio M de N'C. Si b = MC, es evidente
que se cumple la relación anterior, por lo que las circunferencias
con centros B y C y radios BN y MC respectivamente se cortarán
en el vértice A de un triángulo cumpliendo las condiciones
del problema.
Podemos preguntar a Cabri por el lugar geométrico de los puntos A obtenidos de esta forma al fijar BC y variar N dentro de BC.
Parece un arco de circunferencia ...
... pero no.
Si consideramos el segmento BC situado sobre el eje x, y centrado en el origen de coordenadas, podemos hallar la ecuación del lugar geométrico de A:
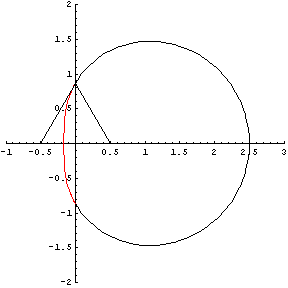Si representamos
esta cuártica vemos que se trata de una "casi circunferencia"
un poco abollada, y vemos que el lugar geométrico de A está
formado por la parte de dicha curva que queda dentro de un triángulo
equilátero construido sobre BC. Naturalmente podriamos haber
construido también A y el triángulo equilátero
al otro lado de BC.
¡Sólo un detalle más antes de cansar al lector! Al
querer hallar los puntos de corte de la curva con el eje x nos llevamos
una sorpresa:
¡Pero la curva parece tener SOLO DOS puntos de corte con el eje x!
Veamos lo que ocurre. Intentemos despejar y en función de
x:
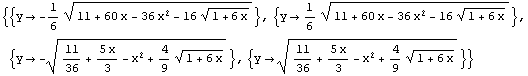
Y veamos el signo de los radicandos:
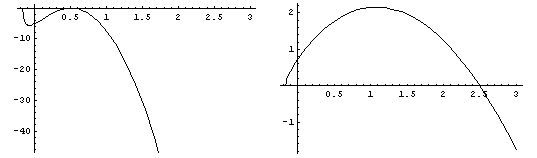
Ahora la situación es clara: uno de los dos radicandos nunca es positivo, y se anula solamente en -1/6 y en 1/2 . Esto dará lugar a sólo dos puntos reales de la curva: el (-1/6,0) y el (1/2,0). Las expresiones de y con el otro radicando son las que dan lugar a la "casi circunferencia", que al contener al punto (-1/6,0) da como resultado que la curva está formada por la "casi circunferencia" y el punto (1/2, 0).
Pulsa aquí para descargar el código de Mathematica utilizado.