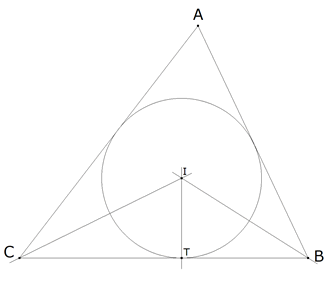
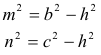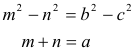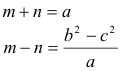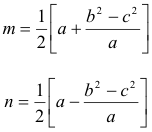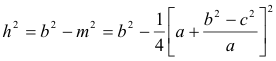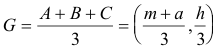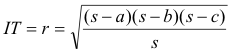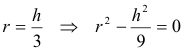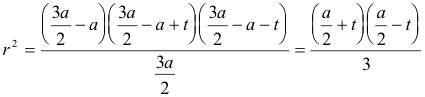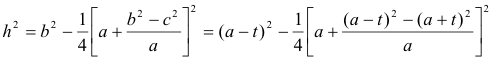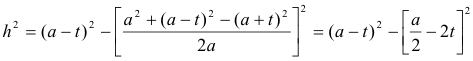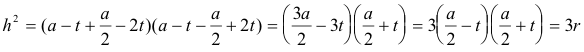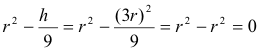Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 234

Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia.

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Pàgina 31. (50)

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de abril de 2005)

INTRODUCCION

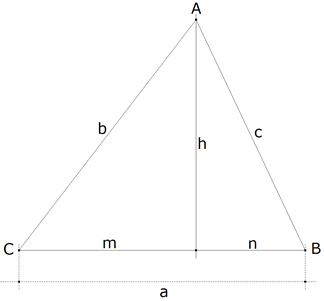
Describiremos sin palabras las relaciones necesarias en un triángulo cualquiera. La condición de lados en progresión aritmética la introduciremos al final.

figura 1  

y de aquí

Y de la figura, podemos representar los vértices como

LAS COORDENADAS DEL BARICENTRO

EL RADIO DEL CIRCULO INSCRITO

figura 2

Recordamos (se ha demostrado varias veces en las páginas de RICARDO BARROSO)

y a partir de las igualdades del tipo anterior se obtiene

SOLUCION

El enunciado nos pregunta lo siguiente:

SI TOMAMOS A COMO TERMINO MEDIO EN LA PROGRESIÓN ARITMÉTICA B,A,C

¿SE CUMPLE QUE EL RADIO DEL CÍRCULO INSCRITO ES UN TERCIO DE LA ALTURA?

Si ello es cierto, esa igualdad se cumplirá para los cuadrados y de aquí vamos a calcular la diferencia

imponiendo la condición de que a, b, c estén en progresión aritmética y a sea el lado medio

y de aquí

y también aplicando sucesivamente que “...diferencia de cuadrados es suma por diferencia...”

Y para acabar

como queríamos demostrar.