Problema 234

Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia.

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Pàgina 31. (50

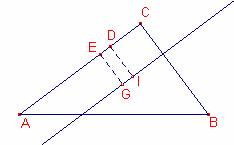
Solución de Ricard Peiró i Estruch:

Sea el triángulo  tal que los lados están en progresión aritmética,

.

Sea I el incentro del triángulo .

Sea G el baricentro del triángulo .

Tenemos que probar que la distancia de I y G al lado  es la misma.

Calculemos el área del triángulo  utilizando la fórmula d’Herón.

 tal que .

.

El área del triángulo  es  donde  es el radio de la circunferencia inscrita en el triángulo.

Entonces,

.

Despejando r:

.

El área del triángulo es la tercera parte del área del triángulo .

Sea  la altura del triángulo .

,    .

Igualando las áreas:

.

Despejando h:

.

Notemos que .

Entonces distancia de I y G al lado  es la misma, por tanto los puntos I, G están sobre una recta paralela al lado .

Con Cabri:

Figure gusiev50.fig

Applet created on 12/04/05 by Ricard Peiró with CabriJava