Propuesto por Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)

Problema 234.- Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia.

Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Pàgina 31. (50)

Solución de  Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.

.-

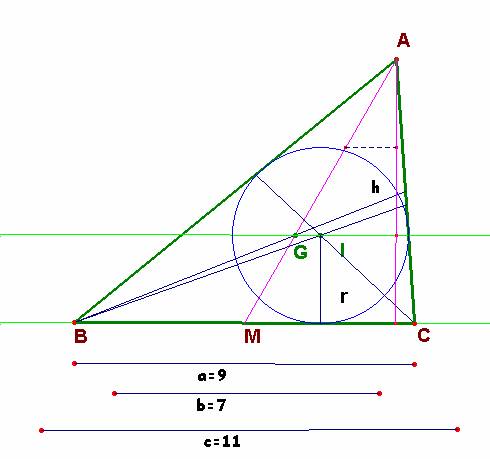
            En un triángulo cualquiera, el baricentro esta situado respecto de un lado a una distancia que es igual a la tercera parte de la altura correspondiente.

El incentro se sitúa a una distancia de ese lado igual al radio de la circunferencia inscrita. Si este radio es igual a la tercera parte de la altura sobre ese lado habremos probado lo que se pretende. Para ello, vamos a calcular el valor de ese radio.

El área del triángulo es igual al semiperímetro por el radio, pero también a la mitad de la base por la altura. Aplicando esto tendremos:

Si los lados del triángulo son b= a-d; a; c=a+d, el perímetro es 2p=3a.

Por tanto  3a·r = a·h, de donde se obtiene que r = h/3, como queríamos demostrar.