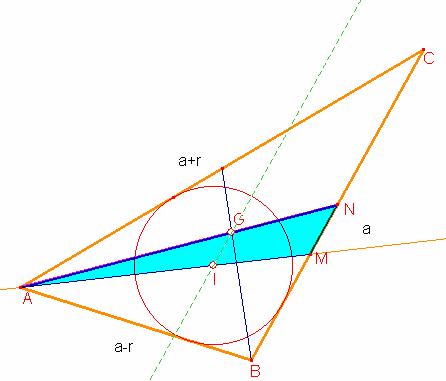
Problema 234
Demostrar que si las longitudes de los lados de un triángulo forman una progresión aritmética, el centro de la circunferencia inscrita en dicho triángulo y el baricentro de éste están situados en una recta paralela al lado de la longitud intermedia.
Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Pàgina 31. (50)
Problema 234
Si els costats d’un triangle formen una progressió aritmètica el centre de la circumferència inscrita del triangle i el baricentre d’aquest jauen en una recta parallela al costat de mesura intermèdia.
Gúsiev , V.y otros (1989) "Prácticas para resolver Problemas matemáticos. Geometría" Ed . Mir . Pàgina 31. (50)
Solución del Prof. William Rodríguez Chamache.
Sea el triángulo ABC de lados en progresión Aritmética, I = incentro , G= baricentro
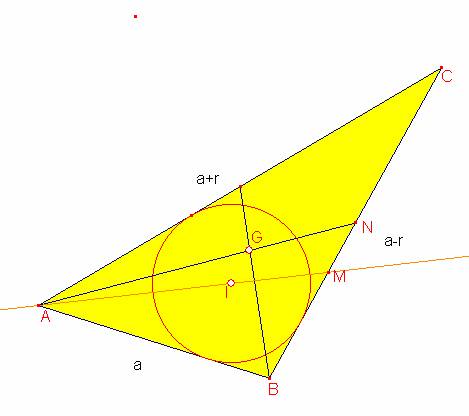
En el triángulo ABC aplicamos el teorema de la bisectriz ![]() reemplazando obtenemos:
reemplazando obtenemos: ![]() .
.
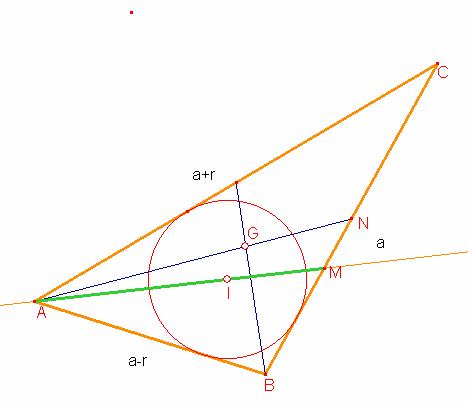
Por otro lado el baricentro divide a cada mediana en la relación ![]()
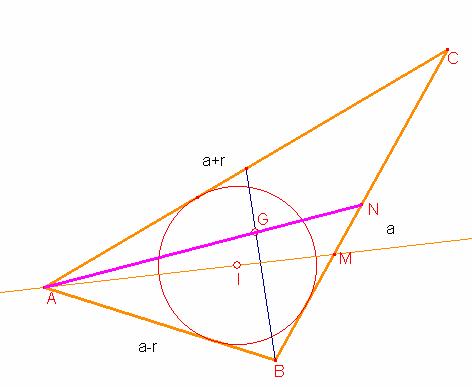
Luego en el triángulo MAN los punto I , G dividen a los lados en la misma razón por lo tanto la recta que pasa por os puntos I , G será paralela al segmento CB (segmento intermedio)