Problema 235
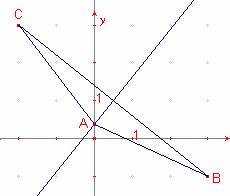
242. La base de un triángulo isósceles ABC es el segmento que une los puntos B(3,-1), C(-2,3) y el vértice A está sobre el eje coordenado yy’. Calcular las ecuaciones de los tres lados del triángulo.
MATEMATICA ELEMENTAL(1948) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº7 y 8
EJERCICIOS ELEMENTALES PROPUESTOS:
Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).
SoluciónRicard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València),
:
Por ser el triángulo 
isósceles de base 
. El vértice A está en la mediatriz del segmento . Calculemos la mediatriz:
.
El punto medio del segmento es 
.
Entonces la recta mediatriz del segmento es:
.
La ecuación del eje de ordenadas es 
.
Resolviendo el sistema formado por ambas recta obtenemos el vértice A.
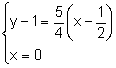, la solución es 
. Entonces, 
.
Calculemos los vectores 
:
.
Determinemos las tres rectas que forman los lados del triángulo:
La recta que pasa por B, C es:
, rBC es y= - 4/5 x + 7/5
La recta que pasa por A, B es:
, 
.
La recta que pasa por A, C es:
, 
.