Problema 236

Construir un triángulo rectángulo conociendo los pies de las tres bisectrices.

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona).
Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Solución:

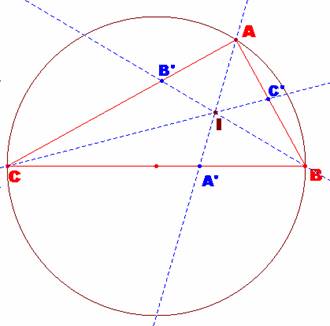
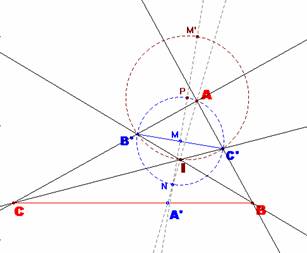
	Sea el triángulo inicial ABC, rectángulo en A.
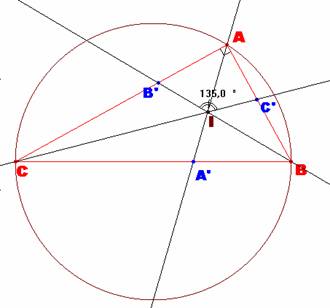
	Observando la figura, nos detenemos en las medidas de los siguientes ángulos notables: <B’AI = <C’AI = 45º y <B’IC’= 135º.

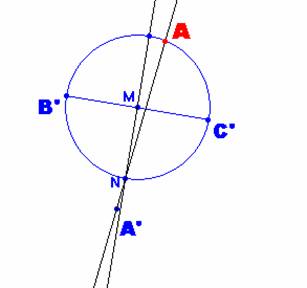
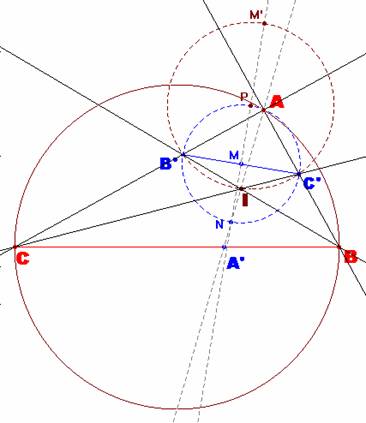
	En este paso, construimos la circunferencia de diámetro B’C’ y el diámetro perpendicular a BC. Este diámetro cortará a la circunferencia en el punto N, La recta A’N cortará a la circunferencia en el vértice A.
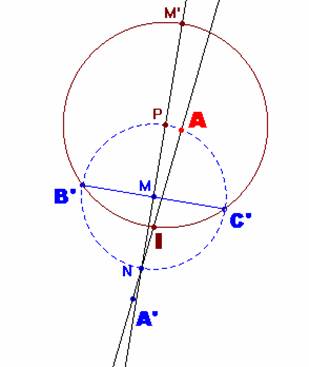
	En este paso, determinamos el punto I, incentro del triángulo inicial ABC. Para ello, construimos el arco-capaz de 135º del segmento B’C’ e intersecamos con la recta AA’, obteniendo así el punto I.
	Construimos las rectas B’I y C’I. Estas rectas cortarán a las rectas AC’ y AB’, en los puntos B y C, respectivamente. Por tanto, tenemos ya determinados los vértices del triángulo ABC inicial.