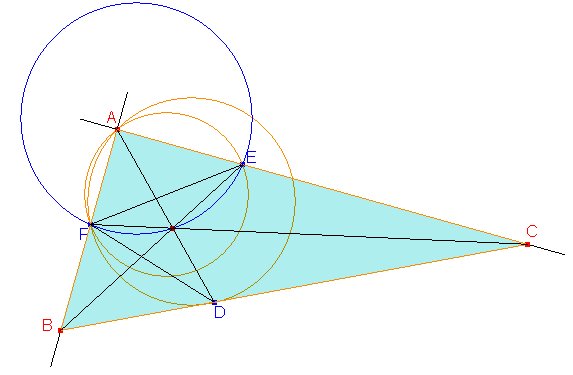
 En la figura de
la derecha mostramos un triángulo rectángulo ABC con sus
bisectrices AD, BE y CF.
En la figura de
la derecha mostramos un triángulo rectángulo ABC con sus
bisectrices AD, BE y CF.
Problema 236 de triánguloscabri |
| 358. Construir un triángulo rectángulo conociendo los pies de las tres bisectrices. |
|
Problemas Gráficos de Geometría. Juan Sapiña Borja. Propuesto por Jose María Pedret. |
Solución de Francisco Javier García Capitán
 En la figura de
la derecha mostramos un triángulo rectángulo ABC con sus
bisectrices AD, BE y CF.
En la figura de
la derecha mostramos un triángulo rectángulo ABC con sus
bisectrices AD, BE y CF.
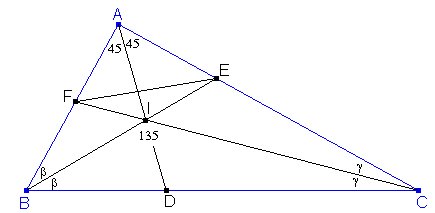
Si sólo conocemos los puntos D, E y F, podemos determinar el vértice A teniendo en cuenta que:
Ahora determinamos el incentro I teniendo en cuenta que desde I se ve el segmento EF bajo un ángulo de 135º, por lo que I estará en la intersección del arco capaz correspondiente con el segmento AD.
Una vez determinado I, podemos trazar las rectas EI y FI que determinarán con las rectas AF y AE, respectivamente los vértices B y C del triángulo buscado.
Observemos que si D, E, F son puntos cualesquiera del plano no estará asegurado que la recta BC contenga al punto D. En efecto, la construcción anterior será la misma si sustituimos el punto D por cualquier otro punto que esté en la recta AI que hemos obtenido a partir de D, E y F.