Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 236.- Construir un triángulo rectángulo conociendo los pies de las tres bisectrices.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid. (Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.

.-

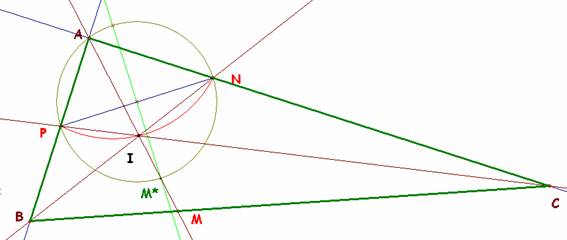             Si son M, N y P los pies de estas bisectrices, siendo el primero de ellos el pie de la bisectriz del ángulo recto, tendremos que el incentro I de este triángulo está sobre el arco capaz del segmento PN y amplitud 135º. A su vez, el vértice A del ángulo recto está sobre el arco capaz de PN y amplitud 90º. Este arco capaz es la circunferencia de diámetro PN.

Según probamos en el problema nº 8 (circunferencia de Euler), la bisectriz de un ángulo y la mediatriz del lado opuesto se cortan en un punto de la circunferencia circunscrita. Aplicando esto, resulta que, cualquiera que sea la posición del vértice A sobre la circunferencia de diámetro PN, su bisectriz se corta con la mediatriz de PN  en un punto fijo, M*. Conocido este punto, hallamos  el vértice A trazando la recta que lo une con M.

Con el vértice A en posición el incentro se calcula de inmediato: la recta AM  contiene a este punto, pero también el arco capaz de PN y amplitud 135º. A partir de aquí la construcción es trivial.