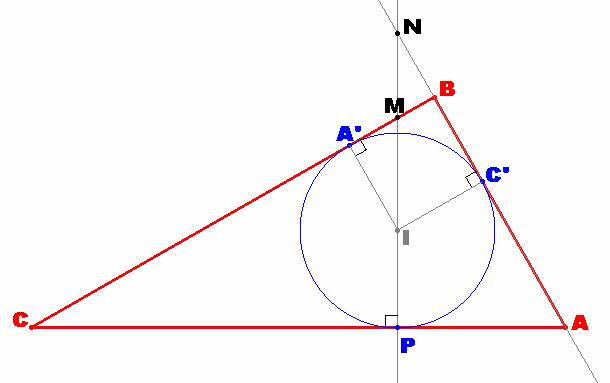
Problema 237
Sea el triángulo ABC, por su
incentro I se traza una perpendicular a AC que corta en M y N a BC y la
prolongación de AB respectivamente.
Si además se cumple que: 1/IM^2 + 1/IN^2 = 1/r^2, donde r = inradio de
ABC, probar que <B=90º.
Propuesto por Juan Carlos Salazar,
profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto
Ordaz).
Salazar, J.C. (2005): Comunicación personal.
Solución de F. Damián Aranda Ballesteros, profesor del
IES Blas Infante de Córdoba.
Solución:
|
|
|
|
A partir de la existencia de
la semejanza entre los siguientes pares de triángulos podemos obtener
algunas relaciones de interés:
De la semejanza entre los
triángulos rectángulos IA’M y CPM, obtenemos que:
![]() (1)
(1)
De la semejanza entre los
triángulos rectángulos IC’N y APN, obtenemos que:
![]() (2)
(2)
Elevando al cuadrado ambas
expresiones y sumándolas entre sí, obtenemos:
![]() (3),
(3),
donde 2s = a + b + c
(perímetro del triángulo ABC).
Como se verifica,
según la hipótesis que ![]() , lo que equivale a la expresión:
, lo que equivale a la expresión:
![]() , significa que, según (3):
, significa que, según (3): ![]()
(s−c)2∙ NA2 + (s−a)2∙
MC2 = NA2∙ MC2
Sustituimos las expresiones anteriores por las igualdades:
NA2
= (s−a)2 + PN2
y
MC2
= (s−c)2 + PM2
(s−c)2∙[(s−a)2 + PN2]
+ (s−a)2∙[(s−c)2 + PM2] =
[(s−a)2 + PN2]∙[(s−c)2 + PM2]
Desarrollando, llegamos a:
2∙(s−c)2∙(s−a)2 +(s−c)2∙PN2 + (s−a)2∙PM2 = (s−a)2∙(s−c)2 + (s−a)2∙PM2 + (s−c)2∙PN2 + PN2 ∙PM2
Esto es,
(s−c)2∙(s−a)2 = PN2 ∙PM2
O, lo que es lo mismo, (s−c)∙(s−a) = PN ∙PM
![]() ; 1=
tagA∙tagC
; 1=
tagA∙tagC
Esta última condición indica que el ángulo B es de
90º ya que:
![]() A+C=
90º; B=90º.
A+C=
90º; B=90º.