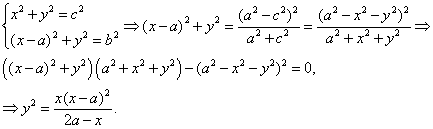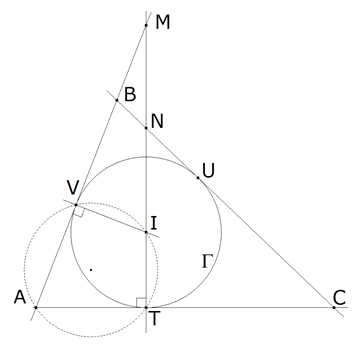
Problema 237 de triánguloscabri

Sea el triángulo ABC, por su incentro I se traza una perpendicular a AC que corta en M y N a BC y la prolongación de AB respectivamente.
Si además se cumple que: 1/IM2 + 1/IN2 = 1/r2, donde r = inradio de ABC, probar que ÐB=90º.

Propuesto por Juan Carlos Salazar.

Solución de Francisco Javier García Capitán

Si seguimos al pie de la letra los datos del enunciado, colocaremos el punto M como en la figura (tomada de la solución de Jose María Pedret), entendiendo la prolongación de AB como la semirrecta que parte de B que no contiene a A.

Al resolver el problema con coordenadas baricéntricas no imponemos a M tal limitación, y lo dejamos estar en cualquier punto de la recta AB. De esta manera, aparecerá una solución para B distinta del ángulo recto vaticinado por el enunciado.

Finalmente, daremos una visión global de todos los triángulos que cumplen la condición que aparece en el enunciado.

1. Cálculos con Mathematica

(Para descargar un cuaderno de Mathematica con estos cálculos, pulsa aquí) .

a. Fórmulas relacionadas con coordenadas baricéntricas que usaremos:

Simplificación de un punto o una recta:

Ecuación de una recta que pasa por dos puntos, o punto de intersección de dos rectas:

Cuadrado de la distancia entre dos puntos:

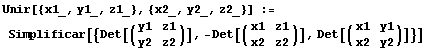
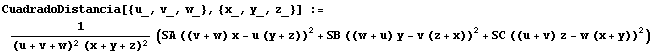
b. Puntos y rectas que intervienen en el problema:

El incentro del triángulo ABC:

El punto de tangencia T de la circunferencia inscrita a ABC con el lado AC:

Las rectas BC y AB

c. Efectuamos los cálculos necesarios:

La recta IT y sus puntos de intersección M y N con con AB y BC, respectivamente.

Obtenemos en forma factorizada la expresión que debe anularese cuando se cumpla el enunciado:

2. Un primer análisis

Vemos rápidamente que el factor corresponde al caso de que el ángulo B sea recto, correspondiendo a la tesis del enunciado, pero observamos que el factor quizás pueda anularse, aportando una nueva solución del problema. Si despejamos b en función de a y c obtenemos dicha solución:

3. Representación de los resultados con Cabri

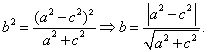
La fórmula anterior parece decir, que para cualesquiera valores de a y c vamos a poder encontrar un valor de b que forme con ellos un triángulo que cumpla las condiciones del enunciado.

Para visualizarlo con Cabri, podriamos fijar un segmento BC de longitud a, y calcular b para este a fijo y para un c variable. Entonces determinariamos A tal que BA=c y CA=b, y observariamos las diferentes posiciones del punto A.

Pero gracias a una sencillísima construcción de Jose María Pedret (gracias de nuevo, Jose María) nos podemos ahorrar el cálculo de b:

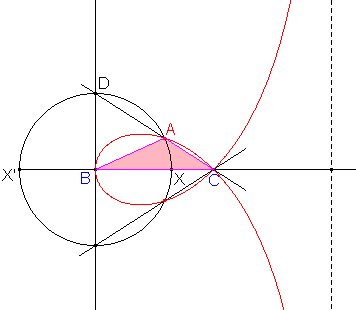Fijamos el segmento BC de longitud a.
Tomamos un punto variable X sobre la semirrecta BC. Será BX=c.
Trazamos la circunferencia con centro B y radio BX, que corta a la perpendicular a BC por B en D.
Entonces A es el punto buscado.

En efecto, usando la potencia de C respecto de la circunferencia,

Usando la herramienta Lugar geométrico de Cabri obtenemos la curva mostrada en la figura.

4. Ecuación de la curva

Terminaremos hallando la ecuación de la curva obtenida. Para ello consideramos a B como origen de coordenadas y a BC como eje x. Entonces, B=(0, 0) y C=(a, 0). Si A=(x, y) entonces

5. Para finalizar ...

La recta tangente a la curva en el origen contiene contiene a los puntos A correspondientes a las soluciones para los que B es recto.
La curva sólo existe si 0 £ x £ 2a, y x=2a es una asíntota de la curva.
En los triángulos solución ABC cuyo vértice A está en la curva, uno de los ángulos A o C es obtuso, por lo que M y N quedan separados por el incentro I.