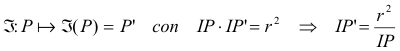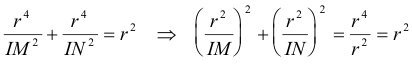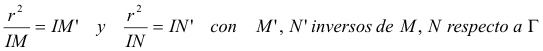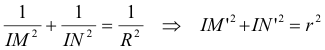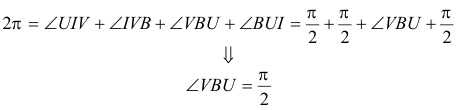Propuesto por Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz) Problema 237 Sea el triángulo ABC, por su incentro I se traza una perpendicular a AC que corta en M y N a BC y la prolongación de AB respectivamente. Si además se cumple que: 1/IM^2 + 1/IN^2 = 1/r^2, donde r = inradio de ABC, probar que <B=90º. Salazar, J.C. (2005): Comunicación personal.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (18 de abril de 2005) |
|
INTRODUCCION |
|
UN CUADRILATERO INSCRIPTIBLE |
|
figura 1
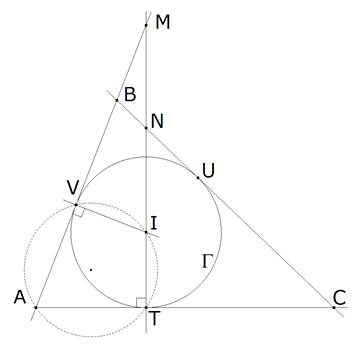
Supongamos que tenemos un triángulo ABC y su círculo inscrito Γ con centro en I. Sean ahora V, U y T los puntos de contacto sobre AB, BC y CA respectivamente. Estudiemos ahora el cuadrilátero AVIT:
Entonces como los ángulos opuestos del cuadrilátero son suplementarios, el cuadrilátero es inscriptible.
|
|
LA INVERSION |
|
Recordemos algo de la inversión. INVERSION (respecto a un círculo) Dado un círculo Γ con centro en I y radio r. Definimos la inversión de un punto P del plano del círculo a la transformación
figura 2
Hay una construcción única que vale tanto si el punto es interior al círculo como si es exterior (Basta saber que los puntos inversos son conjugados respecto al círculo).
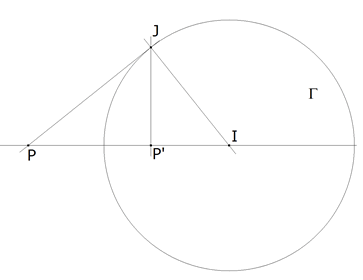
Pero la construcción del punto inverso, que en esta ocasión nos conviene, es la específica según sea el punto interior o exterior al círculo. INVERSO DE UN PUNTO INTERIOR A Γ Sea P’ un punto interior a Γ. Siendo I el centro del círculo, la perpendicular por P’ a la recta IP’ corta al círculo en J. La perpendicular por J a IJ corta a IP’ en P. P y P’ son inversos.
INVERSO DE UN PUNTO EXTERIOR A Γ Sea P un punto exterior a Γ. La tangente por P a Γ toca a este último en J. La perpendicular por J a IP corta en P’ a IP. P’ y P son inversos.
|
|
LA IGUALDAD DEL ENUNCIADO |
|
figura 3
Aún es más, como r es el radio del círculo inscrito si por dos ejes perpendiculares en I trazamos IM”=IM’ e IN’ respectivamente, los puntos U y V que así definimos se halla sobre el círculo inscrito. Por construcción IUM e IVN son rectos y por lo tanto MU y NV son tangentes al círculo.
|
|
SOLUCION |
|
Vamos a trazar un triángulo imponiéndole las condiciones del enunciado.
figura 4
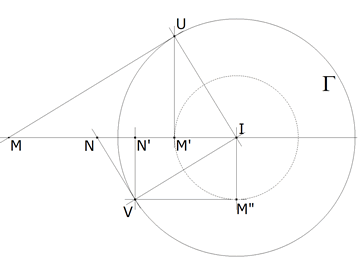
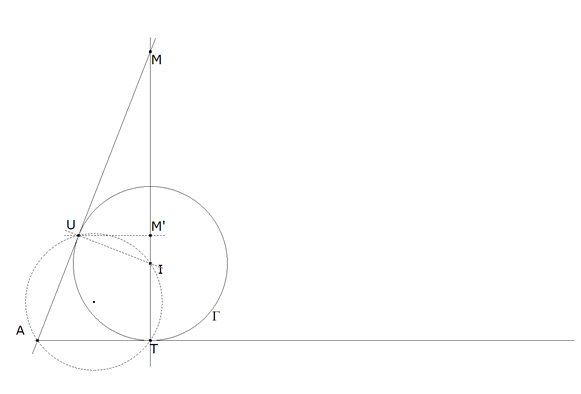
Sea una recta soporte de la base CA del triángulo. Sobre dicha recta tomamos un vértice A y tomemos un punto cualquiera del plano I. Por I una perpendicular a la recta base con la intersección en T. Tomando I como el incentro, IT es el radio del círculo inscrito Γ. T es además el punto de tangencia con el lado CA.
figura 5
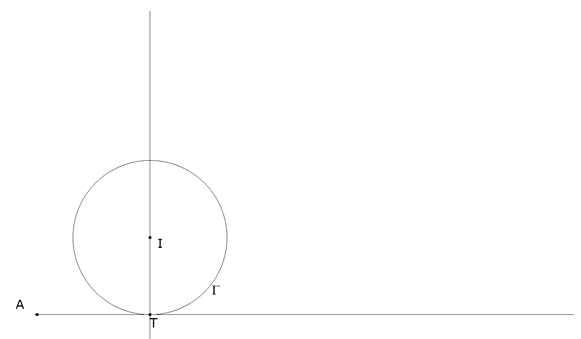
Como hemos visto en la introducción, hallamos el punto de tangencia U por medio del círculo por A, T, I.
figura 6
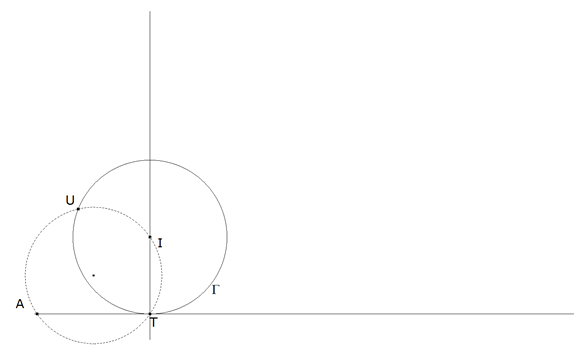
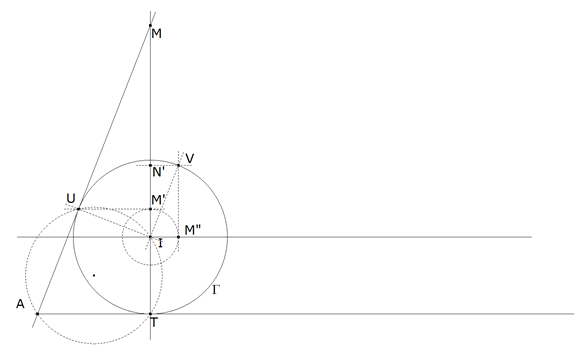
De acuerdo con el enunciado, AU corta a IT en M. Pero de acuerdo con la inversión (ver INTRODUCCION), una paralela por U a AT corta a IT en M’. M’ es el inverso de M respecto al círculo inscrito.
figura 7
IMPONEMOS AHORA LA CONDICION TRANSFORMADA DEL ENUNCIADO (ver INTRODUCCION)
Para ello llevamos IM’ a su perpendicular y obtenemos M”, una paralela por M” a IT corta a Γ en V (el otro punto de contacto) al círculo inscrito. Una paralela por V a AT corta a IT en N’.
figura 8
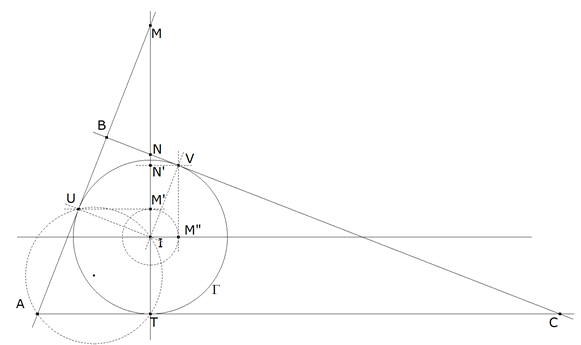
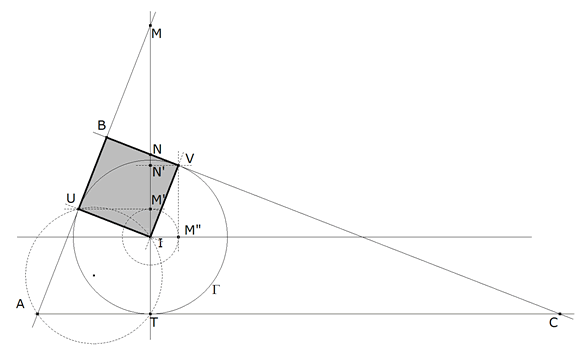
Siendo V el punto de contacto, una perpendicular por V a IV corta a AU en B. VB corta a AT en C y a IT en N.
figura 9
Consideremos el cuadrilátero IUBV. Por construcción de los triángulos rectángulos UM’I e VN’I, se cumple
pero por ser U y V los puntos de tangencia.
Teniendo ahora en cuenta que los ángulos del cuadrilátero deben sumar 2π
que es lo que queríamos demostrar.
|