Problema 237

Salazar, J.C. (2005): Comunicación personal.

Probelma 237

Sea el triángulo ABC, por su incentro I se traza una perpendicular a AC que corta en M y N a BC y la
prolongación de AB respectivamente.
Si además se cumple que: 1/IM^2 + 1/IN^2 = 1/r^2, donde r = inradio de ABC, probar que <B=90º.

Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València)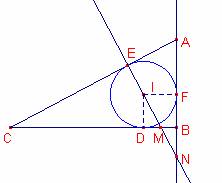

Consideremos el triángulo . Sean D, E, F los puntos de tangencia de la circunferencia inscrita y el triángulo.

La recta perpendicular al lado pasa por el punto de tangencia E.

Por hipótesis del enunciado, esta recta corta el lado en el punto M, entonces el ángulo es agudo.

Los triángulos rectángulos , son semejantes:

.

Aplicando razones trigonométricas al triángulo rectángulo :

.

Los triángulos rectángulos , son semejantes:

.

Aplicando razones trigonométricas al triángulo rectángulo :

.

Por hipótesis: , entonces:

.

.

Entonces, o .

Si , entonces, , por tanto , entonces, .

Si , entonces, lo que es absurdo ya que C es un ángulo agudo.