Problema 237:

Sea el triángulo ABC, por su incentro I se traza una perpendicular a

AC que corta en M y N a BC y la prolongación de AB respectivamente.

Si además se cumple que: 1/IM^2 + 1/IN^2 = 1/r^2, donde r = inradio

de ABC, probar que <B=90º.

Solución: Ver figura:

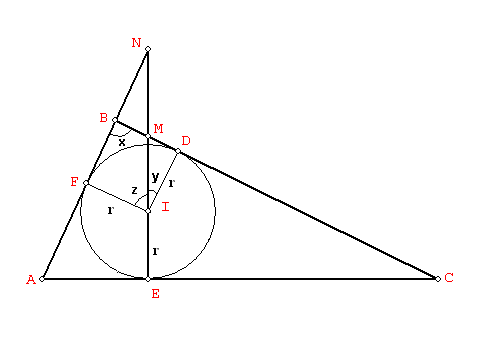
Tenemos que la recta por I, M, N pasa por E punto de tangencia del incirculo con AC. También D, F son puntos de tangencia del incirculo con BC, AB respectivamente.

Además: <MID = y, <NIF = z, 1/IM = cosy /r, 1/IN = cosz /r

Como:

1/IM^2 + 1/IN^2 = 1/r^2

(cosy /r)^2 + (cosz /r)^2 = 1/r^2

(cosy)^2 + (cosz)^2 =1

Entonces: y + z = 90º

Luego en el cuadrilátero BFID:

<B+<F+<I+<D=360º

x+90º+y+z+90º=360º

x+90º+90º+90º=360º

x=90º=<B.