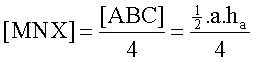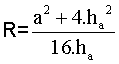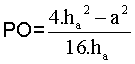Problema 238
Para el aula. Sean M y N los puntos medios tomados
sobre dos lados cualesquiera del triángulo, ABC. Sea X un punto variable
elegido en el otro lado.
Se pide :
a) Demostrar que el triángulo XMN tiene un área que no depende
del punto X, y, que es, 1/4 del área del triángulo ABC.
b) Lugar geométrico descrito por los baricentros y los circuncentros,
respectivamente, cuando X se mueve sobre el lado en que está situado.
Propuesto por Juan Bosco Romero Márquez, profesor colaborador
de
Solución de F.
Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante,
Córdoba (España).
|
|
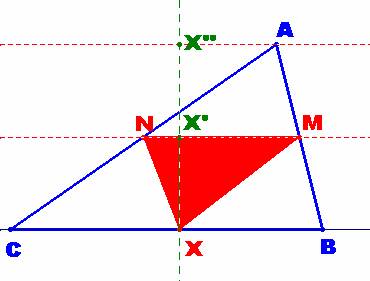
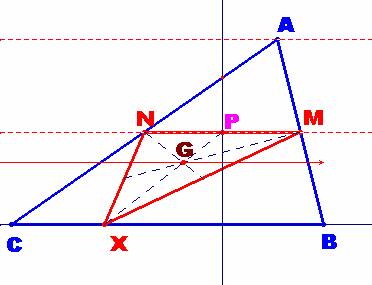
a) El triángulo XMN tiene un área que no depende del punto X, y, que es, 1/4 del área del triángulo ABC. Esto es cierto sin más que tener en cuenta que el lado MN es la paralela media a uno de los lados del triángulo. En la figura representada sería al lado BC.
Entonces, si [ABC] representa el área del triángulo ABC, será:
[ABC]= 1/2∙a∙ha
[XMN]= 1/2∙MN∙(1/2∙ha) = 1/2∙(1/2∙a)∙(1/2∙ha)=1/4∙1/2∙a∙ha=1/4∙[ABC]
Ya que ha=XX’’=2∙XX’
b) Lugar geométrico descrito por los baricentros y los circuncentros, respectivamente, cuando X se mueve sobre el lado en que está situado.
* El lugar geométrico de los baricentros será la recta paralela intermedia entre el lado MN y el lado del triángulo donde está X , situada a una distancia igual a1/3∙(1/2∙ha) a partir del punto P, punto medio de MN.
|
|
* El lugar
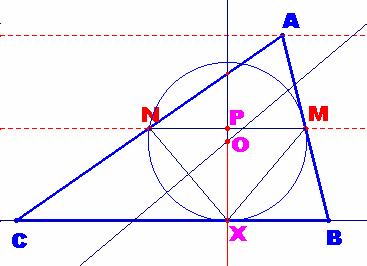
geométrico de los circuncentros será la semirrecta que determina la mediatriz
orientada hacia el tercer lado donde está X a partir del punto O situado a una
distancia del punto medio del segmento MN igual al valor 
. Veamos esto un poco más claro: Puesto que el segmento MN está,
el circuncentro de los triángulos que tienen todos a MN como uno de sus lados
pertenecerá a la mediatriz de MN. Ahora bien la posición límite de este lugar
lo determinará cuando el punto X se
encuentre en la propia mediatriz MN. Cuando esto ocurra, el triángulo MNX será
isósceles y sus lados tendrán las siguientes longitudes
|
|
|
MN= 1/2∙a
Expresando el valor del área del triángulo MNX como:
Sabemos por el epígrafe anterior que: Así, deducimos el valor de R. como:
Y a partir del valor de R, el de PO ya que PO=1/2∙ha − R En definitiva, |
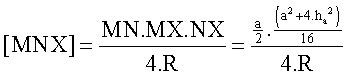, donde R es el valor del radio de la circunferencia
circunscrita al triángulo MNX.
