Problema 238

Sean M y N los puntos medios tomados sobre dos lados cualesquiera del triángulo, ABC.

Sea X un punto variable elegido en el otro lado.

Se pide :

a) Demostrar que el triángulo XMN tiene un área que no depende del punto X, y, que es, 1/4 del área del triángulo ABC.

b) Lugar geométrico descrito por los baricentros y los circuncentros, respectivamente, cuando X se mueve sobre el lado en que está situado.

Romero J.B. (2005): Comunicación personal.

Solución de Jorge Gonzalez Concepción (14 de mayo de 2005)

a)

Al ser M y N puntos medios de los lados respectivamente se tiene que el segmento es paralela media del triángulo ABC, luego su longitud es igual a la mitad del tercer lado, es decir, y además es paralelo al lado , en virtud de esto se tiene que la distancia de cualquier punto X del lado a la recta que pasa por M y N es constante, como que esa distancia es la altura del triángulo XMN respecto a la base se tiene entonces que el área del triángulo MNX es constante para cualquier punto de .

Por otra parte se tiene que como es paralela a y se cortan en C están dadas las condiciones del teorema de las transversales, luego al trazar la altura que pudiera ser como es el caso ilustrado interior o en otro caso exterior, se cumple que los puntos H y D donde corta a las rectas MN y AB respectivamente determinan los segmentos que están en la misma razón que los segmentos , es decir, son iguales de donde podemos afirmar que la altura del triángulo ABC es el doble que el segmento que es la altura del triángulo MNX, luego por un simple cálculo de áreas se obtiene que :

pues , pero se tiene que la

base y que la altura del triángulo MNX, que es la distancia de X

a es la mitad de la altura del triángulo ABC, es decir, . De todo esto

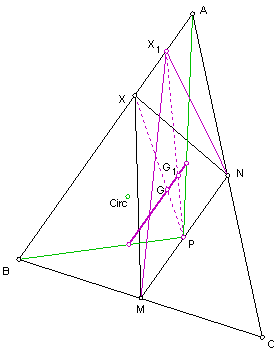
b) El caso del Baricentro que llamaremos G

Como el punto medio P del lado del triángulo MNX permanece fijo y se cumple la relación para el baricentro, se tiene que en el caso del triángulo MNX₁ , donde X₁ es cualquier punto del lado y G₁ es el baricentro de este nuevo triángulo se cumple que: 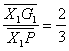y como se cumplen las condiciones del recíproco del teorema de las transversales en su segunda parte, es decir, y además los puntos X, G y P son alineados, así como también los puntos X₁, G₁ y P, se cumple entonces que los puntos G y G₁ determinan una recta que es paralela a la que pasa por A y B, en función de esto los baricentros de los triángulos que se forman al recorrer el punto X el segmento determinan un segmento paralelo a y con extremos en los puntos de intersección de la recta que pasa por G y G₁ con los segmentos que son las medianas de los triángulos extremos que se pueden formar ( Triángulos MNA y MNB) como se ilustra en la figura.

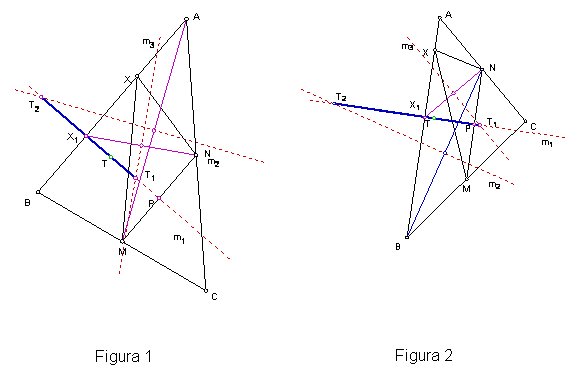
Para el caso del Circuncentro que llamaremos T:

Como el lado del triángulo se mantiene fijo al cambiar la posición de X sobre el lado , obligatoriamente los circuncentros de los triángulos que se formen deben pertenecer a la mediatriz del lado , y describir entonces un segmento perpendicular al lado y por tanto al lugar descrito por la bisectriz, en el punto T₁ se encuentra un extremo del segmento, que es la intersección de la mediatriz m₁ de , con la mediatriz m₃ del lado , cuestión esta que sucede porque el triángulo MNX₁ es isósceles de base .

El otro extremo del segmento descrito por el Circuncentro es el punto T₂, el cual se obtiene como intersección de la mediatriz m₁ del lado con la mediatriz m₂ del lado del triángulo MNA que es el triángulo límite para la determinación de este lugar geométrico.

Resumiendo: El lugar es un segmento perpendicular al lado , cuyos extremos se determinan de la siguiente manera:

- El extremo T₁, se determina como Circuncentro del triángulo MNX, isósceles de base , y X la intersección de m₁ con el lado .

- El extremo T₂ se determina como Circuncentro de uno de los triángulos MNA o MNB, según A o B esté más alejado del punto X₁ de intersección de m₁ con el lado , esto cuando el triángulo no sea isósceles, pues en dicho caso cualquiera de los dos se puede tomar (Figuras 1 y 2)