Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 238

Siguen M, N els punts migs de dos costats qualssevol del triangle .

Siga X un punt variable escollit de l’altre costat.

Es demana:

a) Demostrar que el triangle té un àrea que no depén del punt X, i que és de l’àrea del triangle .

b) Determinar el lloc geomètric descrit pels baricentres i el circumcentres, respectivament quan X varia sobre el costat en el qual està situat.

Romero J.B. (2005): Comunicació personal.

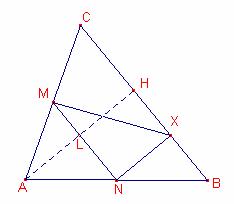
Solució de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):

Siga el triangle . Siga M el punt mig del costat . Siga N el punt mig del costat .

El segment és paral·lela mitjana del triangle .

Siga X un punt sobre el costat .

Siga altura del triangle .

Siga altura del triangle

La distància entre les paral·leles , és .

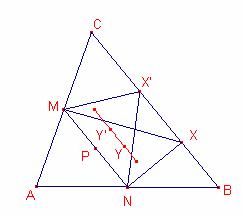
b1)

Siga P el punt mig del segment .

Siguen X, X’ dos punts del costat .

Siguen Y, Y’ els baricentres dels triangles , respectivament.

Per la propietat del baricentre:

Aleshores els triangles , són semblants i la raó de semblança és 3:1. Aleshores els segments , són paral·lels.

La distància de O al segment és de la distància de P al segment .

El lloc geomètric dels baricentres dels triangles al variar X sobre és el segment paral·lel al costat que està entre les semirectes PB, PC i que dista de l’altura del costat .

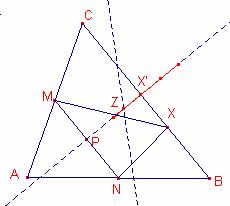b2)

El circumcentre dels triangles està sobre la mediatriu del segment .

El lloc geomètric dels circumcentres dels triangle al variar X sobre és el major dels segments sobre la mediatriu de format pel:

1.- El circumcentre del triangle , X’ intersecció de i la mediatriu de i el circumcentre del triangle .

2.- El circumcentre del triangle , X’ intersecció de i la mediatriu de i el circumcentre del triangle .