Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la
Universidad de Valladolid
Problema 238
Sean M y N los puntos
medios tomados sobre dos lados cualesquiera del triángulo, ABC.
Sea X un punto variable
elegido en el otro lado.
Se pide
:
a) Demostrar que el
triángulo XMN tiene un área que no depende del punto X, y, que es, 1/4 del área
del triángulo ABC.
b) Lugar geométrico
descrito por los baricentros y los circuncentros,
respectivamente, cuando X se mueve sobre el lado en que está situado.
Romero J.B. (2005): Comunicación personal.
.
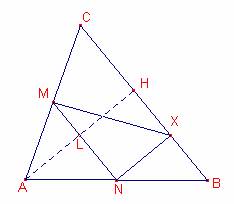
Solución de Ricard Peiró i Estruch Profesor de
Matemáticas del IES 1 de Xest (València):
Sea el triángulo 
. Sea M el punto medio del lado 
. Sea N el punto medio del lado 
.
El segmento 
es paralela media del
triángulo .
.
a)
Sea X un punto sobre el lado 
.
Sea 
altura del triángulo .
Sea 
altura del triángulo 
.
La distancia
entre les paralelas , es 
.
.
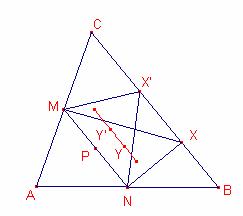
b1)
Sea P el punto medio del segmento .
Sean X, X’ dos puntos del lado .
Sean Y, Y’ los baricentros de los triángulos 
, 
respectivamente.
Por la propiedad del baricentro:
.
Entonces los triángulos 
, 
son semejantes y la razón
de semejanza es 3:1. Entonces los segmentos 
, 
son paralelos.
La distancia de O al segmento es 
de la distancia de P
al segmento 
.
El lugar geométrico de los baricentros de los triángulos al variar X sobre es el segmento paralelo
al lado que está entre las semirectas PB, PC y que dista de la altura del lado .
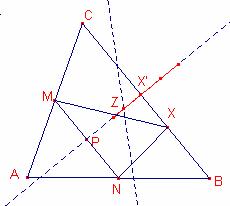b2)
El circuncentro de los triángulos está sobre la mediatriz
del segmento .
El lugar geométrico de los circuncentros de los triángulo al variar X sobre es el mayor de los segmentos
sobre la mediatriz de formado por:
1.- El circuncentro del triángulo , X’ intersección de y la mediatriz de y el circuncentro del triángulo 
.
2.- El circuncentro del triángulo , X’ intersección de y la mediatriz de y el circuncentro del triángulo 
.