Para el aula
Propuesto por Juan Bosco Romero Márquez, profesor colaborador de
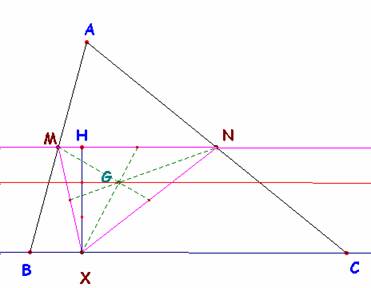
Problema 238 .-Sean M y N los puntos medios tomados sobre dos lados
cualesquiera del triángulo, ABC. Sea X un punto variable elegido en el otro lado.
Se pide :
a) Demostrar que
el triángulo XMN tiene un área que no depende del punto X, y, que es, 1/4 del
área del triángulo ABC.
b) Lugar
geométrico descrito por los baricentros y los circuncentros,
respectivamente, cuando X se mueve sobre el lado en que está situado.
Romero J.B. (2005): Comunicación personal.
Solución de Saturnino
Campo Ruiz, profesor del IES Fray Luis
de León de Salamanca.-
a) El triángulo XMN tiene una base MN
igual a la mitad del lado BC,
siendo su altura sobre ella también igual a la mitad de la altura sobre BC.
Por tanto su área ha de ser la cuarta parte de la de ABC.
b) El baricentro de un triángulo está situado, con
relación a un lado, sobre una paralela a él a una distancia igual a la tercera
parte del valor de la altura sobre ese lado. Ello es así por la propiedad del
baricentro de estar a doble distancia del vértice que del punto medio del lado
opuesto.
Todos los triángulos MNX tienen la misma
altura sobre MN y por ello su baricentro estará sobre una recta paralela
a MN a doble distancia de BC (también paralela) que de MN.
Para determinar el lugar de los circuncentros
observemos que todos ellos han de estar sobre la mediatriz m de MN.
Cada circunferencia con centro en esta mediatriz puede determinar uno de los triángulos MNX si corta a la base BC. Para que esto
suceda, la distancia de su centro a M (o N) ha de ser mayor que
la distancia a BC. En la figura, el punto S no es circuncentro de ningún triángulo MNX, pues no llega
a cortar a BC. Sí lo es, en cambio, el punto R.
La
circunferencia de menor radio que pasa por MNX, con centro en m,
es aquella tangente a la base BC,
o sea la que pasa por el pie P de
su mediatriz. Su centro T se obtiene cortando m con la mediatriz
de NP.

El lugar buscado está formado por todos los puntos
de la semirrecta TP: todos ellos están a mayor distancia de M que de P
( es decir, de BC).