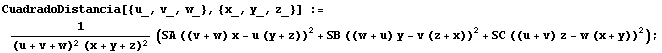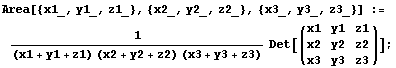Solución
de Francisco Javier García Capitán
Problema 239 de triánguloscabri |
| En el triángulo ABC con
incírculo (I, r) y circuncírculo (O,
R).
Un círculo tangente externamente opuesto al vertice A, es tangente al circuncirculo y AB, AC en A1, D, E. De manera similar para el vértice B tenemos puntos de tangencia B1, F, G con el circuncírculo y AB, BC, y para el vértice C tenemos puntos de tangencia C1, M, N con el circuncirculo y AC, BC. Además las rectas DE, FG, MN conforman el triángulo XYZ. Probar que:
|
|
Propuesto por Juan Carlos Salazar. |
Solución
de Francisco Javier García Capitán
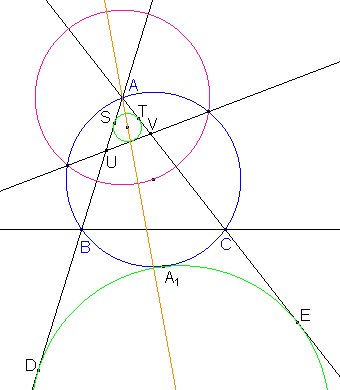
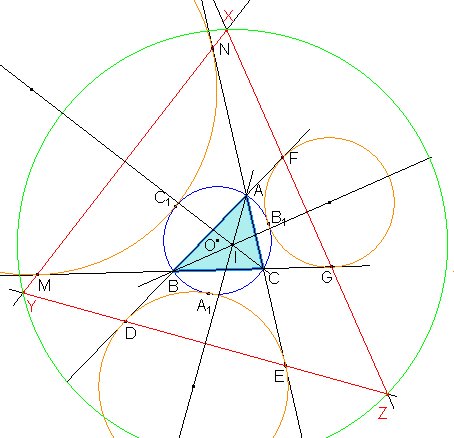
La figura muestra la manera de construir la circunferencia referida al vértice A, usando la inversión.
Consideramos una inversión con centro A y radio R. La circunferencia circunscrita a ABC pasa por el centro de inversión, por lo que se transformará en una recta, concretamente la recta que pasa por los puntos de intersección de ambas. En la figura, esta recta corta a los lados AB y AC en los puntos U y V.
La inversión deja fijas las rectas AB y AC, por lo que la circunferencia buscada se invertirá en la circunferencia inscrita al triángulo AUV. Además, B y C son los inversos de U y V, por lo que los triángulos AUV y ACB son semejantes.
De AU·AB=R2, resulta que AU=R2/c. La razón de semejanza entre los AUV y ACB es entonces R2/bc, por lo que tendremos también AV=R2/b y UV=aR2/bc.
Los puntos D y E serán los inversos de los puntos de conctacto S y T de la circunferencia inscrita a AUV con los lados AB y AC, respectivamente. Llamando s al semiperímetro del triángulo ABC, sabemos que s-a es la distancia del vértice A a los punto de contacto de su circunferencia inscrita con los lados AB y AC, y aplicando la semejanza de los triángulos AUV y ACB tendremos AS = AT =(s-a) R2/bc.
Como hemos dicho D y E serán los inversos de los puntos de conctacto S y T. Entonces AS·AD=R2, de donde AD=bc/(s-a), y el mismo valor se obtiene para AE.
Tenemos:
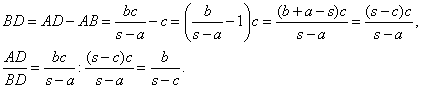
Análogamente, se cumplen las relaciones:
 |
(1) |
Ahora, teniendo en cuenta estas fórmulas para el área del triángulo ABC,
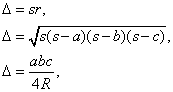
podemos expresar
 |
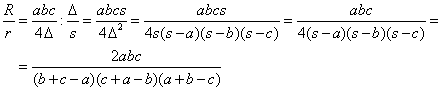(2) |
Teniendo
en cuenta las relaciones de (1) podemos expresar fácilmente las coordenadas
de los puntos que intervienen en el problema.
Ahora hallamos las rectas que los unen:
y los puntos donde se cortan estas rectas:
Una vez calculado todo lo necesario comprobamos que se cumplen las afirmaciones del enunciado:
En primer lugar, los vértices X, Y, Z
están a la misma distancia de I:
El área de XYZ (considerando al área de ABC como
unidad) es 8 veces el cociente R/r que hemos expresado en (2):
Nos cuesta poco comprobar que los triángulos XYZ y ABC
son perspectivos.
También podemos hallar el punto de intersección de AX, BY y CZ, y comprobar que no está en la enciclopedia de Clark Kimberling:
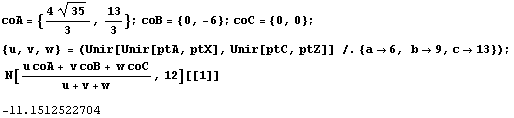
A continuación siguen las funciones de Mathematica que hemos definido y usado para hacer este problema (el código fuente de todas ellas puede descargarse aquí):
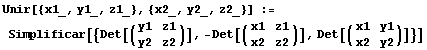
