Problema 239

En el triángulo ABC con incírculo (I, r) y circuncírculo (O, R). Un círculo tangente externamente opuesto al vértice A, es tangente al circuncirculo y AB, AC en A₁, D, E. De manera similar para el vértice B tenemos puntos de tangencia B₁, F, G con el circuncírculo y AB, BC, y para el vértice C tenemos puntos de tangencia C₁, M, N con el circuncirculo y AC, BC. Además las rectas DE, FG, MN conforman el triángulo XYZ. Probar que:

1) I es el circuncentro de XYZ.

2) [XYZ] / [ABC]= 8R/r (donde [XYZ] = área de XYZ)

Solución de Juan Carlos Salazar, profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz)

Sean (O₁), (O₂) y (O₃) los círculos tangentes externos señalados opuestos a los vértices A, B y C respectivamente. A continuación probaremos algunas propiedades que se cumplen en esta configuración geométrica.

En primer lugar probaremos que las rectas GB₁ y NC₁ concurren en un punto del circuncirculo, denominado en este caso X₁.

Si trazamos la recta GB₁ que corta al circuncirculo (O) en X₁, probaremos que X₁ es punto medio del arco CAB. (Ver Fig. 1), esto nos permite concluir que el punto X₁ es el punto de concurrencia de las rectas GB₁ y NC₁.

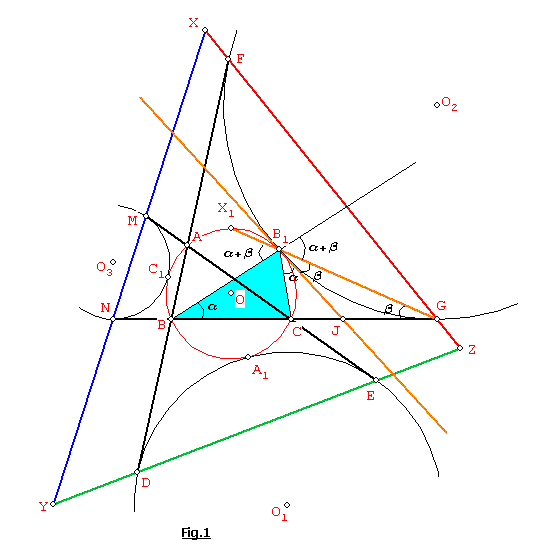
Si trazamos la tangente común por B₁ a los círculos (O) y (O₂) que corta a NG en J, luego: <CB₁J=<B₁BC= a y <JB₁G=<JGB₁= b, además para el triángulo BB₁G tenemos que: <BB₁X₁= <B₁BG+<BGB₁=<B₁BC+<JGB₁=<CB₁J+<JB₁G= a + b =<CB₁G, es decir que GB₁X₁ es bisectriz exterior en B₁ del triángulo CB₁B, ya que <CB₁G= <BB₁X₁= a + b, también: <BB₁X₁= arco CB₁X₁/2 y <CB₁X₁= arco X₁AB/2, por lo tanto X₁ es punto medio del arco BAC. De manera similar podemos probar que para la recta NC₁ su punto de corte con el circuncírculo(O) será el punto medio del arco CAB, es decir el punto X₁, por lo tanto el punto X₁ es el punto de concurrencia de las rectas GB₁ y NC₁.

Por analogía concluimos que los otros pares de rectas EA₁, MC₁ y DA₁, FB₁ también concurren en los puntos Y₁, Z₁ del circuncírculo (O), aún no dibujados.

En segundo lugar probaremos que los excentros I₁, I₂, I₃ del triángulo ABC son los puntos medios de las cuerdas DE, FG y MN.

En referencia al círculo (O₁), EA₁ y DA₁ cortan al circulo (O) en Y₁ y Z₁, donde Y₁Z₁//DE//YZ.(Ver Fig. 2).

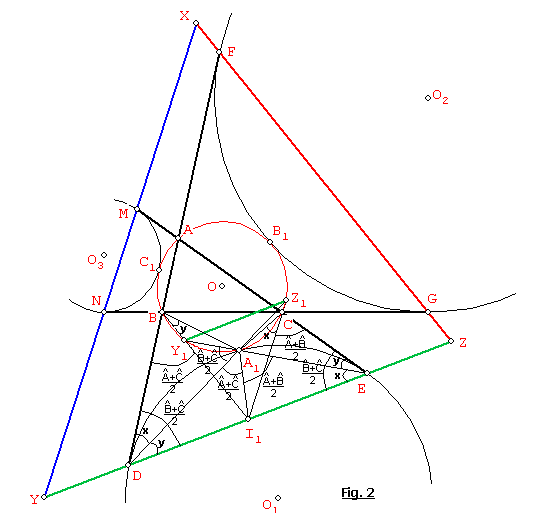
Además Y₁, Z₁ son puntos medios de los arcos ABC y BCA respectivamente. Es decir que BY₁ y CZ₁ son bisectrices exteriores del triángulo ABC. Si I₁ es el punto de corte de BY₁ con DE (YZ), probaremos que I₁ es excentro de ABC.

Como <I₁BD=<I₁BC= (<A+<C)/2 y <ADE = <DEA= x + y = (<B+<C)/2

Donde: x = <BDA₁= <A₁ED e y = <CEA₁= <EDA₁

En el triángulo DBI₁:

<DI₁B+<BDI₁+<I₁BD=180º

<DI₁B+<ADE + (<A+<C)/2=<DI₁B + (<B+<C)/2 + (<A+<C)/2= 180º

<DI₁B= (<A+<B)/2

Luego el cuadrilátero DI₁A₁B es cíclico, ya que: <DA₁B= arco BA₁Z₁/2= arco BCA/2= (2<A + 2<B)/4 = (<A + <B)/2 = <DI₁B.

También: <I₁A₁D=<I₁BD= (<A + <C)/2, luego: <BDA₁=<I₁DA₁=<A₁EC= y, además: <A₁DB= <A₁ED=<A₁CI₁=x.

Para el triángulo A₁DE:

<A₁DE+<DEA₁+<EA₁D= y + x +<EA₁D = (<B + <C)/2 + <EA₁D= (<B + <C)/2 + <I₁A₁D + <I₁A₁E= (<B + <C)/2 + (<A + <C)/2 + <I₁A₁E= 180º.

Luego: <I₁A₁E= (<A + <B)/2.

Suponemos que el punto corte de Z₁C con DE es I₁’ (no dibujado), luego: <I₁’CA₁= arco A₁CZ₁/2= <A₁Y₁Z₁ = < A1ED = x y también < I₁’CE = (<A + <B)/2 debido a que Z₁C es bisectriz exterior en C del triángulo ABC.

Por lo tanto el cuadrilátero A₁I₁EC es cíclico, debido a que:

< E I₁A₁ + <A₁CE= <I₁A₁D + <I₁DA₁ + < A₁CI₁’+ < I₁’CE = (<A + <C)/2 + y + x + (<A + <B)/2 = (<A + <C)/2 + (<B + <C)/2 + (<A + <B)/2 =180º.

Esto nos conduce a que el punto I₁’ coincide con el punto I₁, ya que: < I₁’CE=< I₁A₁E = (<A + <B)/2.

Por lo tanto las bisectrices exteriores CZ₁ y BY₁ se cortan en el punto I₁ (excentro de ABC). Además en el triángulo isósceles ADE como AI₁ es bisectriz, también es mediana y se cumple que I₁ es punto medio de DE. Para los excentros I₂, I₃ el procedimiento es similar, es decir también se cumple que I₂, I₃ son puntos medios de FG, MN respectivamente.

A continuación procedemos a conformar la figura integral (Fig.3) del problema considerando todos los círculos y excentros.

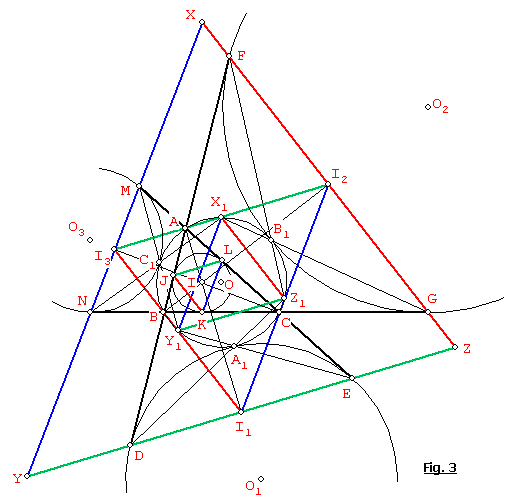
Por todo lo expuesto, tenemos que (GB₁, NC₁), (EA₁, MC₁), (DA₁, FB₁), se cortan en X₁, Y₁, Z₁ sobre el circuncírculo (O). Además X₁Z₁//FG//XZ y X₁Y₁//MN//XY, es decir que X₁Y₁Z₁ y XYZ son homotéticos.

Debido a que AX₁, BY₁, CZ₁ son bisectrices exteriores del triángulo ABC, se cumple que AX₁//DE//YZ, ya que <X₁AC= <X₁AF= <AED= <ADE= (<B+<C)/2, de forma similar: BY₁//FG//XZ y CZ₁//MN//XY. En otras palabras el triángulo I₁I₂I₃ es el triángulo mediano del triángulo XYZ, debido a que sus lados son paralelos a los lados del triángulo XYZ (anticomplementario).

Conocemos que el triángulo I₁I₂I₃ (excentral) de ABC tiene un circuncirculo de radio 2R, es decir que el radio del ciruncirculo de XYZ es 4R, por ser triangulo anticomplementario del triángulo I₁I₂I₃. Considerando además el incirculo del triángulo ABC, cuyos puntos de tangencia con los lados AB, BC, CA son J, K, L, también tenemos que el triángulo JKL es homotético con los triángulos X₁Y₁Z₁, I₁I₂I₃ y XYZ.

De todo lo expuesto el incentro del triángulo ABC es el ortocentro del triángulo I₁I₂I₃, como el triángulo I₁I₂I₃ es el triángulo mediano del triángulo XYZ, luego I es el circuncentro de XYZ.

Conocemos las siguientes relaciones:

[JKL] / [ABC] = (r) / (2R)… (1)

[X₁Y₁Z₁] / [JKL] = (R²) / (r²)… (2)

[XYZ] / [X₁Y₁Z₁] = (4R)² / (R)² = 16… (3)

A partir de (1), (2) y (3):

[XYZ] / [ABC] = 8R/r QED.