Problema 240
Los tres lados de un triángulo están expresados en metros por tres números consecutivos. Determinar el radio del círculo inscrito y el área del triángulo, sabiendo que el ángulo mayor es el doble del menor.

MATEMATICA ELEMENTAL (1947) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española.

4ª Serie – Tomo VII nº2 (Ejercicio Propuesto por: Ayudantes de Telecomunicaciones. ) Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante, Córdoba (España).

Sean x−1; x ; x+1; los lados del triángulo a construir. Por lo dicho en el enunciado, sus ángulos opuestos vendrán dados por los valores a ; 180−3a ; 2∙a, respectivamente.

Por el teorema de los senos, tendremos:

Es decir:

Si ahora utilizamos el teorema del coseno para el lado menor, x−1, tenemos que:

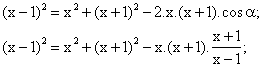
Quitando denominadores, obtenemos la ecuación de segundo grado:

Por tanto, la única solución válida será x=5.

Así los lados del triángulo en cuestión serán de 4, 5 y 6 m.

Veamos que, en efecto, se verifica que el ángulo mayor es el doble del menor. Para ello, consideramos el valor de cos2∙a y cosa.

Según ya hemos visto, ;

Así entonces:

Por otro lado, según el teorema del coseno para el ángulo mayor A se tiene que A=2∙a, tenemos:

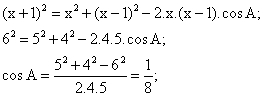
Como quiera que: cos2∙a= 2∙cos²a −1, se verificará que:

cos2∙a = 2∙(3/4)² −1= 2∙9/16−1 =9/8−1= 1/8 = cos A

En definitiva, 2∙a= A, c.q.d.

Una vez que ya sabemos que los lados del triángulo son 4, 5 y 6; los datos que se nos solicitan son fáciles de calcular.

Si llamamos 2s=a+b+c, perímetro del triángulo ABC, entonces 2s=15 m.

Así el área del triángulo será:

[ABC]=m²

Radio de la circunferencia inscrita, r, verificará que [ABC]=r.s, de donde 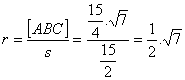m