Problema 240

Los tres lados de un triángulo están expresados en metros por tres números consecutivos. Determinar el radio del círculo inscrito y el área del triángulo, sabiendo que el ángulo mayor es el doble del menor.

Solución de Julio A. Miranda Ubaldo Profesor del Matemáticas

Huaral (Perú) 12 de Mayo del 2005

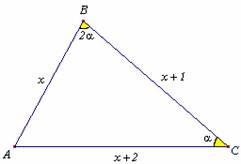
De acuerdo al enunciado del problema efectuamos el siguiente gráfico:

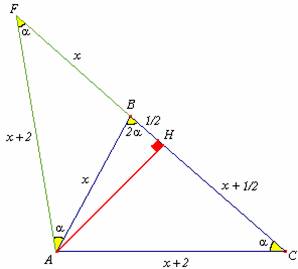
Prolonguemos CB hasta F de modo tal que BF = AB, luego el triángulo AFB es isósceles ,así mismo se puede observar que el triángulo FAC también es isósceles, precisamente desde el vértice A del triángulo FAC tracemos la altura AH entonces

CH = HF pero como CF = 2x + 1 entonces CH = x + ½ entonces HB = ½. (ver figura)

Aplicando el teorema de las proyecciones en el triángulo ABC tendremos :

AH =

de donde deduce que

Luego las medidas de los lados del triángulo ABC son : AB = 4 ; BC = 5 y AC = 6.

Ahora calculemos el área del triángulo ABC usando la fórmula de Herón:

A = = . .......(1)

De otro lado podemos calcular el área del mismo triángulo usando la siguiente fórmula:

A = siendo “ p ” el semiperímetro del triángulo y “ r ” el inradio .

A = ....(2) Igualando (1) y (2) tendremos que : r = .