Problema 240

Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

Problema 240

622. Los tres lados de un triángulo están expresados en metros por tres números consecutivos. Determinar el radio del círculo inscrito y el área del triángulo, sabiendo que el ángulo mayor es el doble del menor.

MATEMATICA ELEMENTAL (1947) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española

4ª Serie – Tomo VII nº2 (Ejercicio Propuesto por: Ayudantes de Telecomunicaciones. )

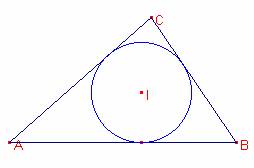
Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València).

Siga el triángulo , , .

Aplicando el teorema de los senos al triángulo :

, . Simplificando:

.

Aplicando el teorema del coseno al triángulo :

.

. Simplificando:

. Resolviendo la ecuación:

.

Entonces los lados del triángulo son: .

Calculemos el área del triángulo utilizando la fórmula de Herón:

.

El área del triángulo es: donde r es el radio de la circunferencia inscrita y p el semiperímetro del triángulo. Entonces:

. Resolviendo la ecuación: .