Propuesto por Maite
Peña Alcaraz, estudiante de Industriales en
Problema
240.- 622.
Los tres lados de un triángulo están expresados en metros por tres números consecutivos.
Determinar el radio del círculo inscrito y el área del triángulo, sabiendo que
el ángulo mayor es el doble del menor.
MATEMATICA ELEMENTAL (1947) Revista
publicada por el instituto Jorge Juan de matemáticas y
4ª Serie –
Tomo VII nº2 (Ejercicio Propuesto por: Ayudantes de
Telecomunicaciones. )
Solución de Saturnino Campo Ruiz, profesor del IES Fray
Luis de León de Salamanca.-
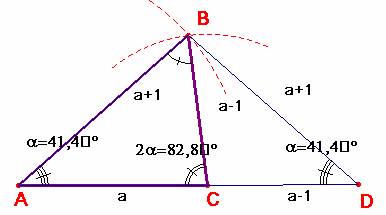
Llevando a continuación de a = AC,
el lado BC = a –1 como muestra la figura, se forma el
triángulo isósceles CBD, en el
cual los ángulos iguales CBD y
CDB miden igual que el ángulo e BAC, resultando de ello que también
es isósceles el triángulo ABD.
Un razonamiento sobre
las áreas de los triángulos ABC y ABD nos conducirá a la solución
del problema.
Estos triángulos tienen la misma altura desde B, por tanto, la
razón de sus áreas es la de las bases correspondientes: 
. De otra parte, el ángulo ABD y el ACB
son suplementarios. La razón de las áreas es también igual a la razón de los
productos de los lados de esos ángulos, es decir: 
. Igualando ambas y simplificando, resulta la ecuación
2a-1 = 
cuyas soluciones son a=0
(que no es válida obviamente) y a=5, que es la solución del
problema. Los lados del triángulo buscado miden 4, 5 y
Para hallar el valor del área recurrimos a la fórmula de Herón. El semiperímetro es igual
a 7,5. El área vale Área (ABC)
=
=
. El radio del círculo
inscrito es igual al área dividida por el semiperímetro,
esto es, r=
.