Problema 241 de triánguloscabri

Solución de Francisco Javier García Capitán

Análisis:

Si en la fórmula general de la bisectriz del ángulo B:

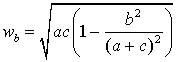
sustituimos llegamos fácilmente a la relación:

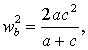
es decir, el lado c debe ser solución de la ecuación de segundo grado:

Las soluciones de esta ecuación serán dos longitudes (positiva, la que nos interesa) y (negativa) tales que

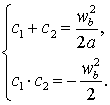
Para obtener tales longitudes existe un procedimiento general. Este procedimiento puede encontrarse, por ejemplo, en Geometría Superior de Bruño (17ª edición, página 261).

En primer lugar debemos construir un segmento que tenga por longitud la mitad de la suma deseada para y , es decir

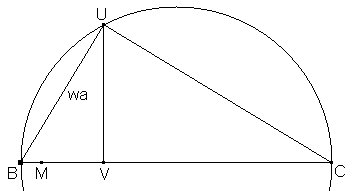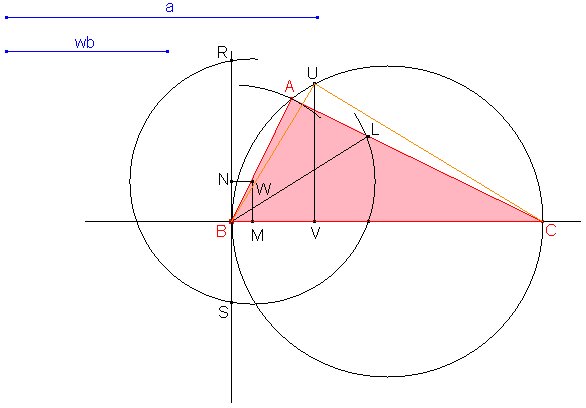
Para ello, dibujamos un triángulo rectángulo BUV rectángulo en U con hipotenusa BC=a y Los triángulos semejantes BUV y BCU nos dan

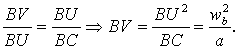
Por tanto, dividiendo el segmento BV en cuatro partes, obtendremos un punto M tal que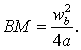

Ahora debemos buscar dos números m y n cualesquiera tales que por ejemplo nosotros elegimos:

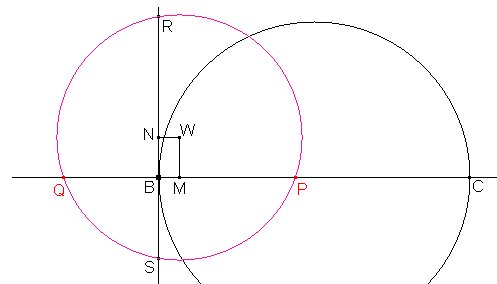
Representamos estos valores en una recta perpendicular a BM, tomando como origen el punto B. Como los valores son opuestos, los representamos en sentidos opuestos: BR=m, BS=n.

Ahora obtenemos el punto medio N de RS y hallamos la intersección W de las perpendiculares a BM por M y a BN por N.

Con centro en W trazamos la circunferencia que pasa por R y S, que determinará los puntos P y Q sobre el eje BM.

Los segmentos BP y BQ son las soluciones buscadas. A nosotros nos interesa BP, que será el lado c del triángulo rectángulo que pedía el enunciado. Trazando una circunferencia con centro B y radio BP, ésta cortará a la circunferencia con diámetro BC en vértice A del triángulo buscado.