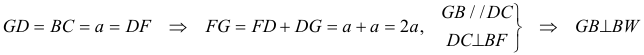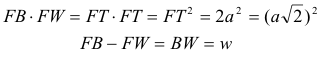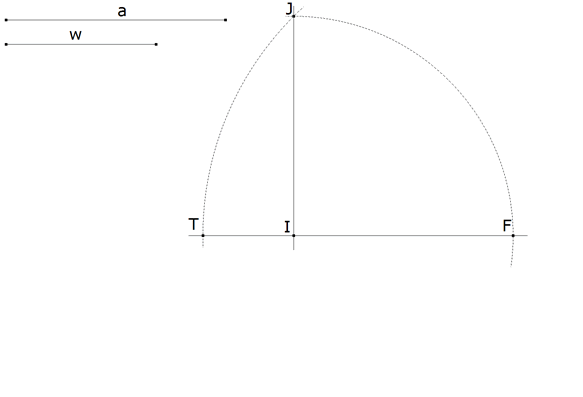Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 241

432. Construir un triángulo rectángulo conociendo la hipotenusa a y la bisectriz del ángulo B.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de mayo de 2005)

INTRODUCCION

Las ideas fundamentales de esta solución proceden del texto de JUAN SAPIÑA BORJA

 PROBLEMAS GRAFICOS DE GEOMETRIA. Litograf Madrid (1955)

SUPONGAMOS EL PROBLEMA RESUELTO

figura 1

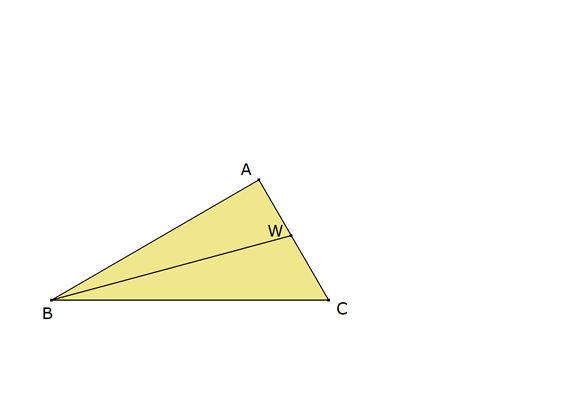
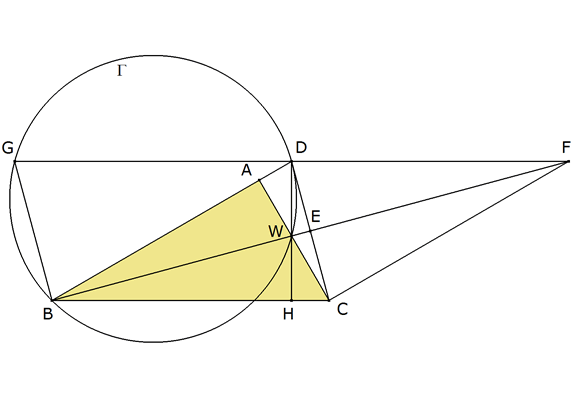
Supongamos que ABC es el triángulo buscado, rectángulo en A.

La bisectriz del ángulo B corta al lado CA en W.

figura 2

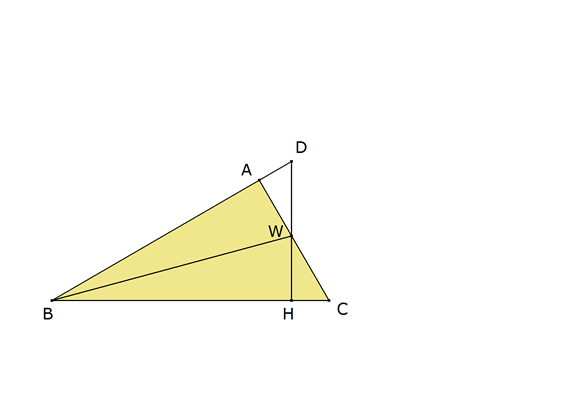
Trazamos por W la perpendicular al lado BC que es cortado por el punto H.

WH corta al lado AB en D.

Como BW es la bisectriz

Y por construcción

Los triángulos BWA y BWH tienen dos ángulos iguales y un lado común y por lo tanto son iguales.

Podemos repetir el razonamiento para la igualdad de los triángulos WHC y WAD

Y de aquí

figura 3

Por lo visto en la figura 2, el triángulo CBD es isósceles con

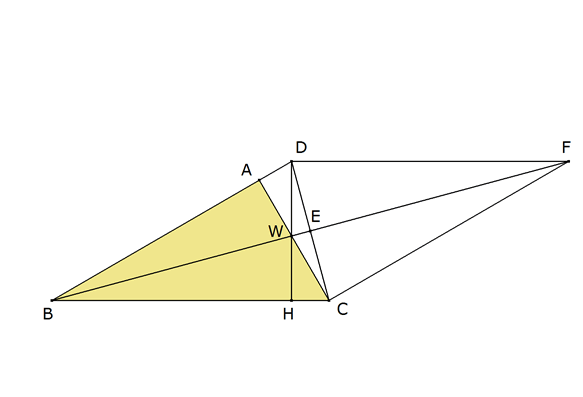
Con una paralela por D a BC y una paralela por C a AB, podemos pues completar el rombo DBCF. Este rombo nos asegura que

También nos asegura que DC y BF son ortogonales y se cortan en E.

figura 4

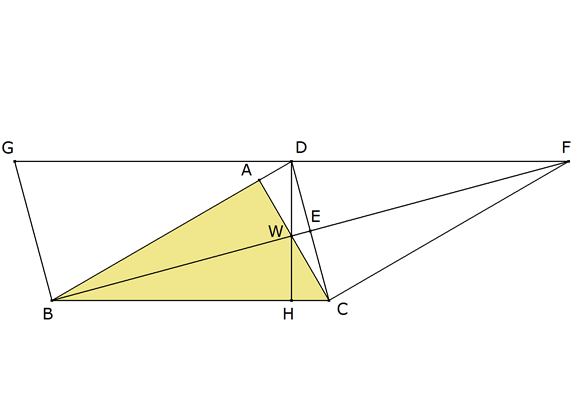
Con una paralela por D a BC y con una paralela por B a CA, completamos el paralelogramo DCBG

Consideremos ahora el cuadrilátero GBWD

Es decir, dos ángulos opuestos del cuadrilátero son complementarios

y por lo tanto el cuadrilátero GBWD es inscriptible en un círculo Γ.

figura 5

Trazado el círculo Γ, expresamos la potencia del punto F respecto a Γ.

Pero por otra parte

Es decir, nuestro problema se reduce a la búsqueda de dos segmentos de los que conocemos su producto y su diferencia.

HALLAR DOS SEGMENTOS DE PRODUCTO Y DIFERENCIA CONOCIDAS

figura 6

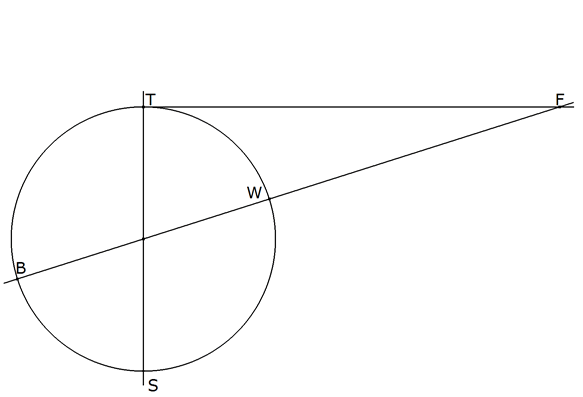
Calculando la potencia de F respecto al círculo BTW

Basta pues tomar, sobre una recta por F, un punto T tal que

donde FT es la diagonal de un cuadrado de lado a. Tangente a T trazamos una circunferencia de diámetro TS=BW=w.

B y W se obtienen mediante la intersección de la circunferencia con una recta por F y el centro de la circunferencia anterior.

LA SOLUCION

figura 7

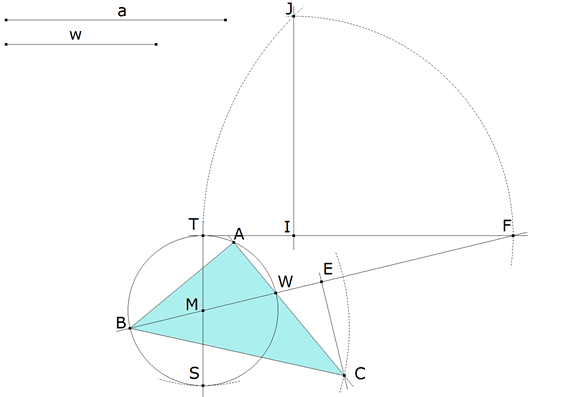
Sea a la hipotenusa dada y w la bisectriz del ángulo B.

Tomemos I, un punto cualquiera del plano, y por él una recta cualquiera.

figura 8

Con centro I trazamos un arco de círculo de radio a que corta a la recta en F y a una perpendicular por I en J.

Con centro en F, círculo de radio FJ que corta a FI en T

figura 9

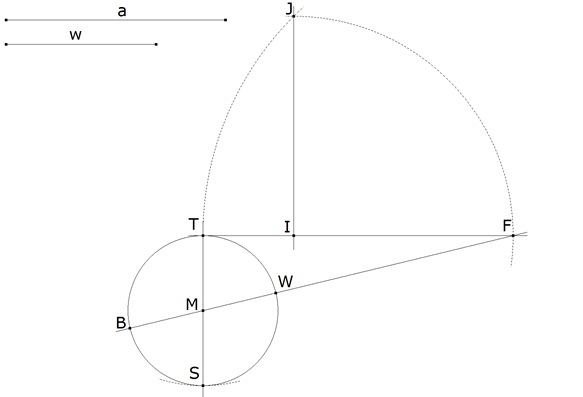
Por T una perpendicular a IF y sobre ella un punto S tal que

Trazamos el círculo de diámetro TS cuyo centro es M. FM corta al círculo en W y B.

Hemos obtenido FB, Como hemos visto en la introducción, FB es la diagonal de un rombo singular.

figura 10

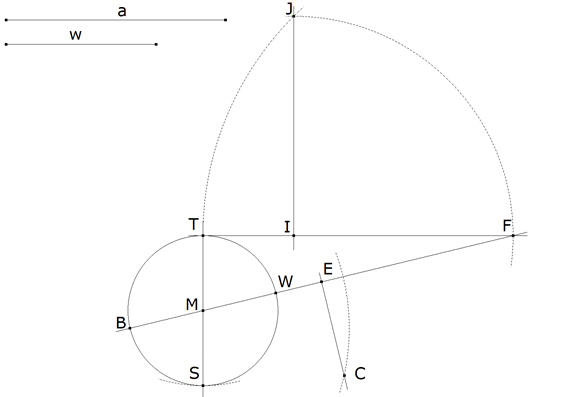
La otra diagonal del rombo estará en la mediatriz de FB. Las dos diagonales se cortan en E.

Con centro en B trazamos un arco de círculo de radio a que corta a la mediatriz de FB en C.

figura 11

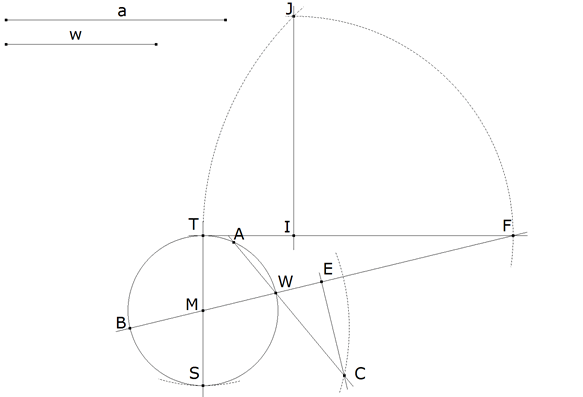
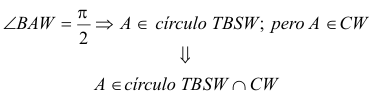
Para hallar A podemos atajar, ya que

Y por tanto la recta por C y W vuelve a cortar al círculo en A.

figura 12

ABC es el triángulo buscado. Habría otra solución que sería la simétrica de ABC respecto FB.