Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 241

432. Construir un triángulo rectángulo conociendo la hipotenusa a y la bisectriz del ángulo B.

Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (2 de mayo de 2005)

Las herramienta básica para estas DOS SOLUCIONES que presento es la herramienta lugar de CABRI II PLUS.

La otra herramienta básica es la de realizar la solución prescindiendo de una de las condiciones del enunciado; para reintroducirla más tarde.

PRIMERA SOLUCION

figura 1

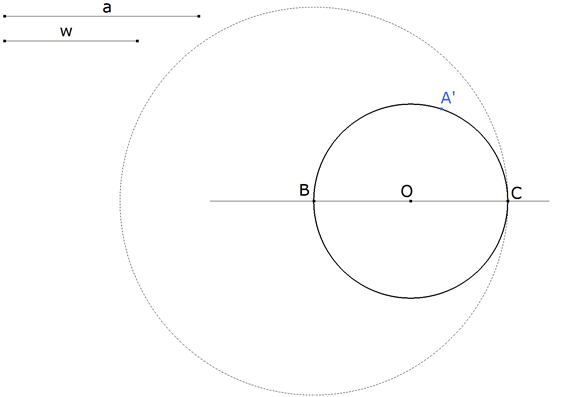
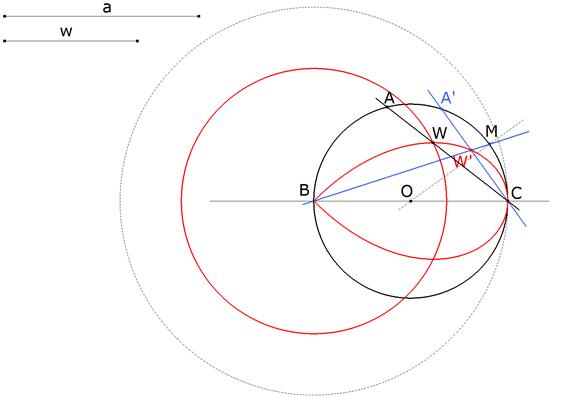
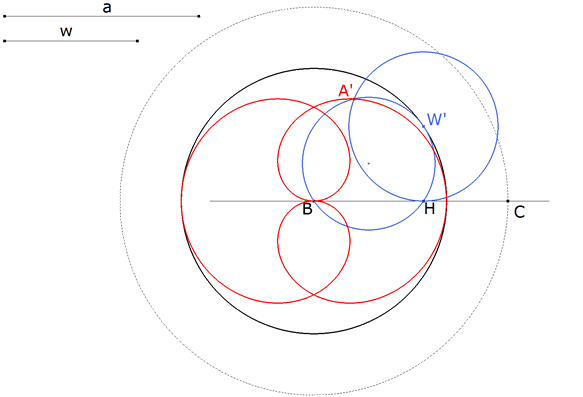
Dadas la hipotenusa a y la bisectriz w, PRESCINDIMOS DE LA CONDICIÓN de que la bisectriz es igual a w.

Con centro en B, un punto cualquiera del plano, trazamos el círculo de radio a.

Tomamos sobre este círculo un punto C y trazamos el círculo de diámetro BC.

El centro del círculo es O, punto medio de BC.

Para completar un triángulo rectángulo cualquiera tomamos un punto A’ sobre este último círculo.

figura 2

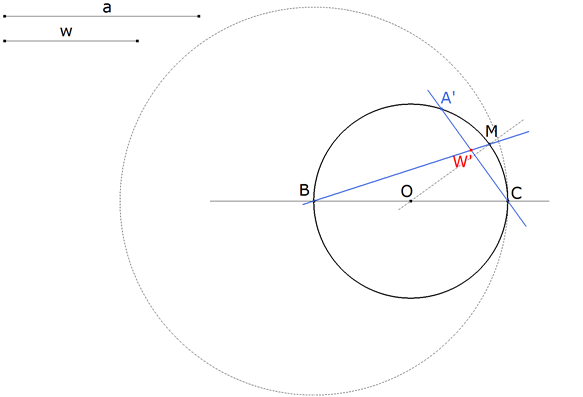
Hallemos ahora W’ el pie de la bisectriz de B sobre el lado CA’. Para ello basta recordar que la bisectriz pasa por el punto medio M del arco opuesto. (Hay quien lo enuncia diciendo que la bisectriz y la mediatriz del lado opuesto se encuentran sobre el círculo circunscrito).

BM corta al lado CA’ en W’.

figura 3

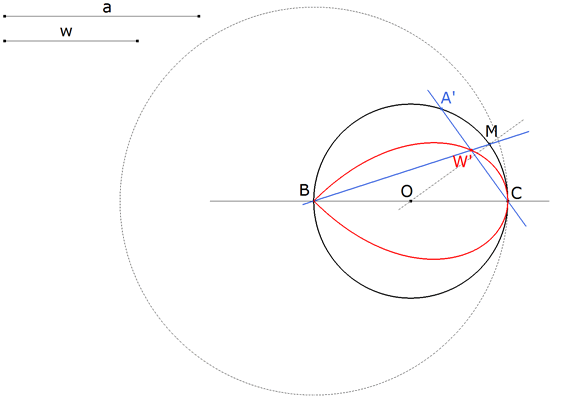
Desplazando A’ sobre el círculo de diámetro BC obtenemos distintas posiciones de W’.

Con CABRI II PLUS obtenemos el lugar geométrico de W’ cuando A’ se desplaza sobre su círculo.

figura 4

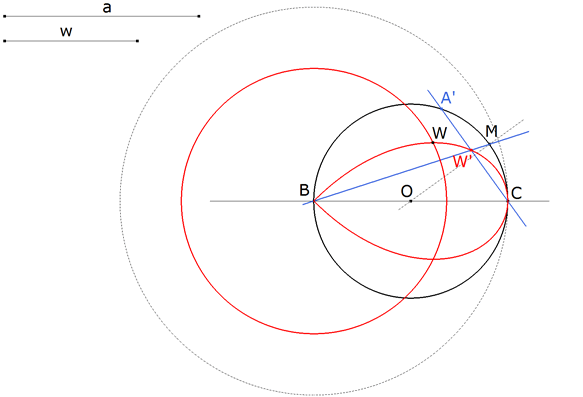
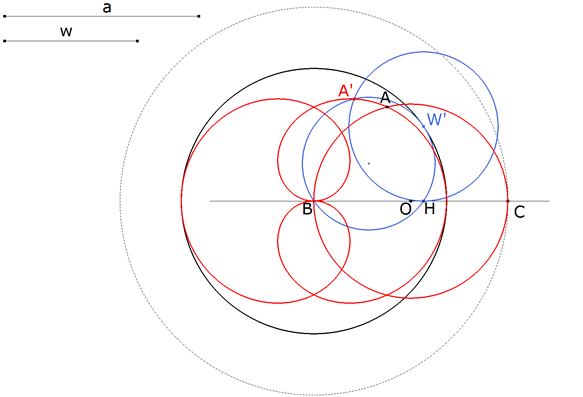
REINTRODUCIMOS AHORA LA CONDICIÓN de que la bisectriz mide w; por lo tanto W estará sobre el círculo de centro B y radio w. Como a su vez W está sobre el lugar geométrico de los pies W’, W estará en la intersección de ambos.

figura 5

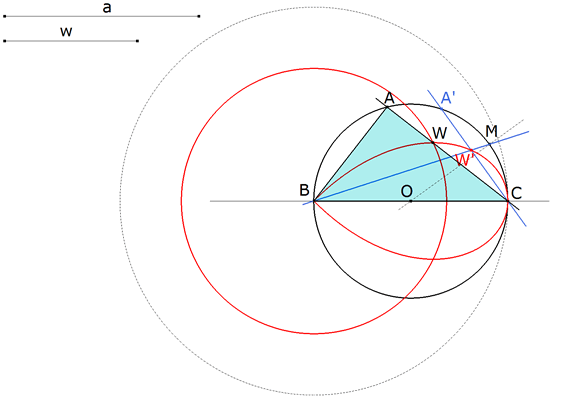
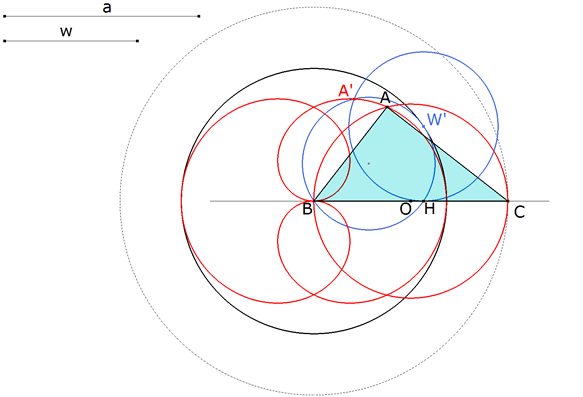
Podemos determinar A como la intersección de CW y el círculo de diámetro BC.

figura 6

ABC es el triángulo buscado. Habría otra solución que sería la simétrica de ABC respecto a BC.

SEGUNDA SOLUCION

figura 7

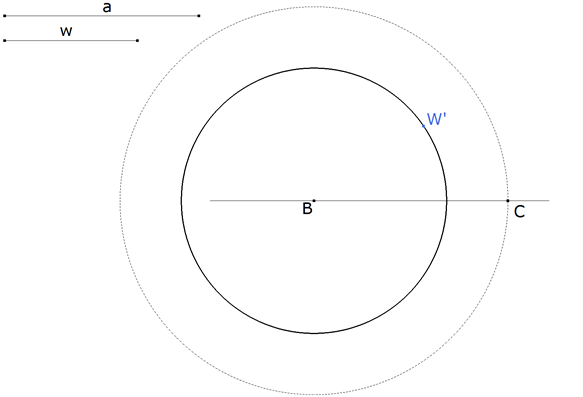
Dadas la hipotenusa a y la bisectriz w, PRESCINDIMOS DE LA CONDICIÓN de que el triángulo sea rectángulo.

Con centro en B, un punto cualquiera del plano, trazamos el círculo de radio a.

Tomamos sobre este círculo un punto C.

Con centro en B, Trazamos un círculo de radio w.

Para completar un triángulo cualquiera tomamos un punto W’ sobre este último círculo.

figura 8

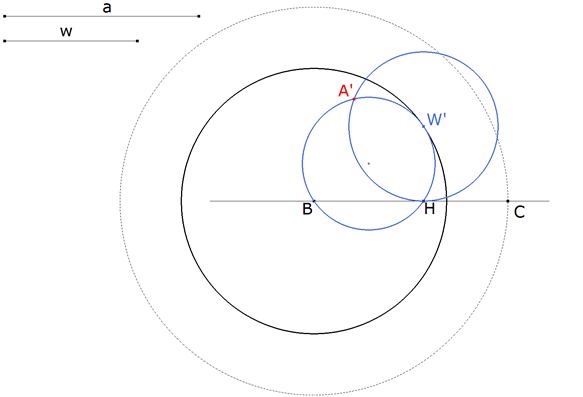
Imponemos ahora que BW’ es la bisectriz del ángulo B

Pero además A’ está sobre el círculo de diámetro BW’ con lo que

figura 9

Desplazando W’ sobre el círculo de centro B y radio w obtenemos distintas posiciones de A’.

Con CABRI II PLUS obtenemos el lugar geométrico de A’ cuando W’ se desplaza sobre su círculo.

figura 10

REINTRODUCIMOS AHORA LA CONDICIÓN de que el triángulo buscado es rectángulo; por lo tanto A estará sobre el círculo de diámetro BC. Como a su vez A está sobre el lugar geométrico de los vértices A’, A estará en la intersección de ambos.

figura 11

ABC es el triángulo buscado. Habría tres soluciones más. En total cuatro, tantas como intersecciones de los dos lugares.