Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

Problema 241.- 432 Construir un triángulo rectángulo conociendo la hipotenusa y la bisectriz del ángulo B. Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid. (Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León de Salamanca.- El teorema de Pitágoras aplicado al triángulo rectángulo BAW nos permite calcular el valor de la bisectriz de B, w=BW , pues el cateto AW, según el teorema de la bisectriz, mide AW= y por tanto w² =AW² + c². Efectuando los cálculos oportunos y eliminando el valor del cateto b (gracias al teorema de Pitágoras), se obtiene finalmente: w² = (1)

En esta expresión sólo se desconoce el valor de c, que está ligado a los de a y w por la ecuación que resulta de (1) al quitar denominadores: 2ac² ─ w²c ─ w²a = 0 (2).

La solución positiva de esta ecuación es el valor del cateto c, lo cual, junto con la hipotenusa, permitiría realizar la construcción pedida. Veamos cuál es esta solución:

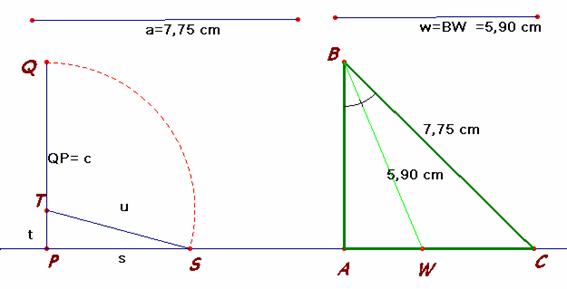
c =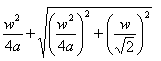 (3)

Para que la expresión (3) quede más sencilla vamos a poner s=; t=; u=, con lo que tendremos:

c = t + u. (4)

Construyendo los segmentos s y t podremos construir u y tener resuelto el problema.

De la definición de t deducimos que , por tanto el segmento 2t es cuarto proporcional entre w, 2a y w y su construcción es inmediata a partir del teorema de Thales:

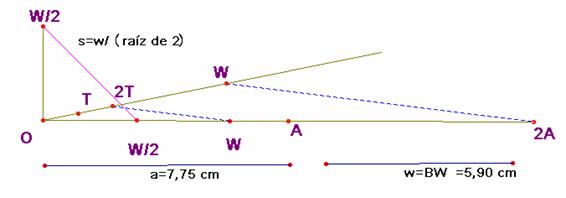
También es inmediata la construcción del segmento s= (segmento color rosa).

u es la hipotenusa de un triángulo de catetos s y t. Para construir c basta con llevar el segmento u a continuación de t. Con ello ya podemos abordar la construcción del triángulo rectángulo ABC.