Problema 242 de triánguloscabri

Sean ABC un triángulo, y AA', BB' y CC' tres cevianas arbitrarias que concurren en el punto interior del triángulo P', distinto del centro de gravedad.
Sean los puntos A", B" y C" sobre los lados BC, AC y AB, respectivamente, tales que: CA'=A"B, AB'= B"C y AC'= C"B. Probar que :
a) Las cevianas AA", BB" y CC" concurren en un punto P".
b) Si definimos los puntos A* como intersección de las rectas C´B" y C"B´, B* como intersección de las rectas A'C" y A"C' y, C* como la intersección de las rectas B'A" y B"A', probar que los puntos A*, B* y C* están alineados y que la recta A*B*C* pasa por los puntos P' y P".
c) Calculad el cociente de las razones dobles de los cuatro pares de puntos siguientes: (A*, B*, C* ,P'):(A*,B*, C*, P").
d) ¿Qué sucede si P' = G, centro de gravedad del triángulo?
Bonus:
e) ¿En qué casos alguno de los puntos A*, B*, C* es un punto del infinito, por ser paralelas las rectas que lo definen?
f) ¿Qué punto P' de partida debemos tomar si queremos que el baricentro G pertenezca a la recta A*B*C*?

Propuesto por Juan Carlos Salazar.

Solución de Francisco Javier García Capitán

La figura de la derecha muestra los puntos P' y P", que se se llaman conjugados isotómicos.

Que las cevianas AA", BB" y CC" concurren en un punto P", como afirma el apartado a), y que sirve para dar validez a la definición anterior, puede demostrarse muy fácilmente usando el teorema de Ceva. Sin embargo, contando con que otros compañeros usarán este teorema, recurriré al uso de las coordenadas baricéntricas para resolver este problema.

Preliminares

Los cálculos con ecuaciones baricéntricas para resolver este problema no son muy complicados. De todas formas, estas serían las instrucciones para realizar con Mathematica. El código fuente con todas las instrucciones puede descargarse pulsando aquí.

Partimos de que

Un punto o una recta pueden representarse ambos como una terna de números.
Dos ternas son equivalentes si una es múltiplo de la otra. Por eso usamos Simplificar para obtener la expresión más sencilla.
El mismo procedimiento Unir nos sirve para hallar el punto de intersección de dos rectas y la ecuación de la recta que une dos puntos.

$Simplificar[{u_, v_, w_}] := Simplify[{u, v, w}/PolynomialGCD[u, v, w]]$
$Unir[{x1_, y1_, z1_}, {x2_, y2_, z2_}] := Simplificar[{Det[({{y1, z1}, {y2, z2}})], -Det[({{x1, z1}, {x2, z2}})], Det[({{x1, y1}, {x2, y2}})]}]$

a) Las cevianas AA", BB" y CC" concurren en un punto P".

Introducimos las coordenadas de los vértices del triángulo de referencia:

Ahora, las coordenadas del punto P' y de sus correspondientes trazas A', B' y C'. Las coordenadas de A', B' y C' pueden obtenerse a partir del concepto de coordenadas baricéntricas, o bien como intersección de la recta que une P' con un vértice y el lado opuesto.

Las coordenadas de los puntos A", B" y C" se obtienen permutando coordenadas en A', B' y C':

Ahora comprobamos que AA", BB" y CC" concurren en un punto.

Det[{Recta[ptA, ptA2], Recta[ptB, ptB2], Recta[ptC, ptC2]}]

Obtengamos las coordenadas del punto de intersección P":

b) Si definimos los puntos A* como intersección de las rectas C´B" y C"B´, B* como intersección de las rectas A'C" y A"C' y, C* como la intersección de las rectas B'A" y B"A', probar que los puntos A, B y C* están alineados y que la recta ABC* pasa por los puntos P' y P".

Hallemos las coordenadas de los puntos A*, B* y C*:

${-u^4 + v^2 w^2, u v (-u^2 + w^2), u (-u^2 + v^2) w}$
${u v (-v^2 + w^2), -v^4 + u^2 w^2, v (u^2 - v^2) w}$
${u w (v^2 - w^2), v w (u^2 - w^2), u^2 v^2 - w^4}$

Comprobamos que estos tres puntos están alineados:

Hallamos los coeficientes de la ecuación de la recta A*B*C*:

${u (-v^2 + w^2), v (u^2 - w^2), (-u^2 + v^2) w}$

Sustituimos las coordenadas de P' y P", para ver que son puntos de la recta:

c) Calculad el cociente de las razones dobles de los cuatro pares de puntos siguientes: (A, B, C* ,P'):(A,B, C*, P").

Necesitamos la complicada fórmula del cuadrado de la distancia entre dos puntos. Una vez, introducida, la usamos para definir otra función que calcula el cuadrado de la razón doble de cuatro puntos.

$CuadradoDistancia[{u_, v_, w_}, {x_, y_, z_}] := 1/((u + v + w)^2 (x + y + z)^2) (SA ((v + w) x - u (y + z))^2 + SB ((w + u) y - v (z + x))^2 + SC ((u + v) z - w (x + y))^2) ;$

CuadradoRazonDoble[P_, Q_, R_, S_] := Divide[CuadradoDistancia[P, R]/CuadradoDistancia[Q, R], CuadradoDistancia[P, S]/CuadradoDistancia[Q, S]]

Factor[CuadradoRazonDoble[ptA3, ptB3, ptC3, ptP1]/CuadradoRazonDoble[ptA3, ptB3, ptC3, ptP2]] 

Podemos entonces interpretar que el cociente de las razones dobles es

d) ¿Qué sucede si P' = G, centro de gravedad del triángulo?

P' y P" coinciden, y los puntos A*, B* y C* quedan indeterminados.

e) ¿En qué casos alguno de los puntos A, B, C* es un punto del infinito, por ser paralelas las rectas que lo definen?

Consideremos el caso, por ejemplo, del punto A*, cuyas coordenadas hemos visto que son:

${-u^4 + v^2 w^2, u v (-u^2 + w^2), u (-u^2 + v^2) w}$

Se tratará de un punto del infinito si sus coordenadas suman 0. Usamos la función Tr (traza) de Mathematica para sumar todas las coordenadas y Factor para ver más fácilmente cuando se anula la expresión resultante.

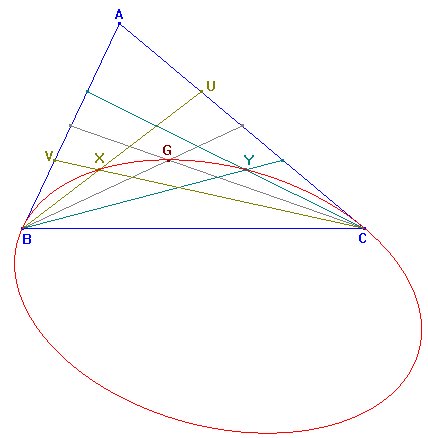
Al tratarse de un punto interior al triángulo el único factor que puede anularse es el último. Vemos que se trata de una cónica, por se un polinomio de segundo grado. Es evidente que pasa por los puntos B y C, y por el baricentro G. Para representarla rápidamente con Cabri, podemos hallar otros dos puntos, por ejemplo los puntos X=(2,4,1) e Y=(2,1,4).

La ceviana BX corta a AC en el punto U=(2,0,1), cumpliendo CU:UA=2:1, y la ceviana CX corta a AB en el punto V=(2:4:0)=(1:2:0), cumpliendo AV:VB = 2:1. Análogamente podemos hallar el punto Y.

Podemos ver en la figura obtenida, y podemos razonar fácilmente a partir de la ecuación, que las cónica tiene por tangentes los lados AB y AC del triángulo

En el siguiente applet, el punto P' varía en la cónica (una elipse) hallada anteriormente y vemos cómo las rectas B'C" y B"C' que definen el punto A* son paralelas.

f) ¿En **qué punto P' de partida debemos tomar si queremos que el baricentro G pertenezca a la recta ABC*?**

Sustituimos las coordenadas del baricentro G en la recta A*B*C*, y obtenemos la expresión en u, v, w que debe anularse:

Puede comprobarse fácilmente que cada uno de los factores corresponde a una de las medianas del triángulo ABC.

En el applet que sigue P' varía en la mediana que pasa por B, y vemos que A* y C* coinciden con el punto medio del lado AC:

Problema 242 de triánguloscabri

Preliminares

a) Las cevianas AA", BB" y CC" concurren en un punto P".

b) Si definimos los puntos A* como intersección de las rectas C´B" y C"B´, B* como intersección de las rectas A'C" y A"C' y, C* como la intersección de las rectas B'A" y B"A', probar que los puntos A*, B* y C* están alineados y que la recta A*B*C* pasa por los puntos P' y P".

c) Calculad el cociente de las razones dobles de los cuatro pares de puntos siguientes: (A*, B*, C* ,P'):(A*,B*, C*, P").

d) ¿Qué sucede si P' = G, centro de gravedad del triángulo?

e) ¿En qué casos alguno de los puntos A*, B*, C* es un punto del infinito, por ser paralelas las rectas que lo definen?

f) ¿En qué punto P' de partida debemos tomar si queremos que el baricentro G pertenezca a la recta A*B*C*?

b) Si definimos los puntos A* como intersección de las rectas C´B" y C"B´, B* como intersección de las rectas A'C" y A"C' y, C* como la intersección de las rectas B'A" y B"A', probar que los puntos A, B y C* están alineados y que la recta ABC* pasa por los puntos P' y P".

c) Calculad el cociente de las razones dobles de los cuatro pares de puntos siguientes: (A, B, C* ,P'):(A,B, C*, P").

e) ¿En qué casos alguno de los puntos A, B, C* es un punto del infinito, por ser paralelas las rectas que lo definen?

f) ¿En **qué punto P' de partida debemos tomar si queremos que el baricentro G pertenezca a la recta ABC*?**