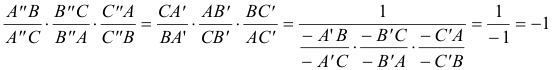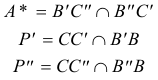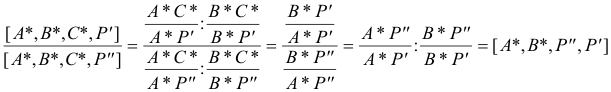Problema 242. Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Sea ABC un triángulo, y AÁ, BB́ y CĆ tres cevianas arbitrarias que concurren en el punto interior del triángulo Ṕ, donde éste no puede ser el centro de gravedad del triángulo dado. Á, B́y Ć, son sus pies sobre los lados BC, AC y AB, respectivamente.

Sean los puntos A", B" y C" sobre los lados BC, AC y AB, respectivamente, tales que :

CÁ=A"B, AB́= B"C y AĆ= C"B.

Probar que :

a) Las cevianas AA", BB" y CC", concurren en un punto P".

b) Si definimos los puntos A* como intersección de las rectas ĆB" y C"B́, B* como intersección de las rectas ÁC" y A"Ćy, C* como la intersección de las rectas B́A" y B" Á, probar que los puntos A* B* C* están alineados y que la recta A*B*C* pasa por los puntos Ṕy P".

c) Calculad el cociente de las razones dobles de los cuatro pares de puntos siguientes:

(A*,B*,C*,Ṕ)/(A*.,B*.C*.P").

d) ¿Qué sucede si P'=G, centro de gravedad del triángulo?

Romero, J.B. (2005): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de mayo de 2005)

TEOREMA DE CEVA

Para que tres rectas que pasan respectivamente por los tres vértices del triángulo ABC sean concurrentes, es necesario y suficiente que sus puntos de intersección A’, B’, C’ con el lado opuesto al vértice correspondiente verifiquen la siguiente relación

figura 1

TEOREMA DE PAPPUS

figura 2

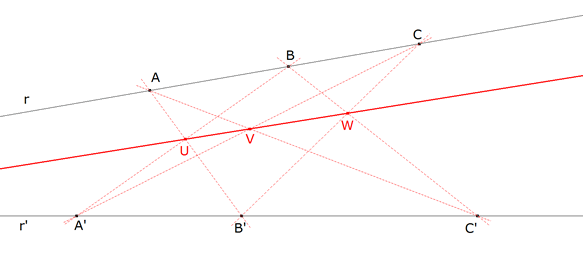
Sean r, r’ dos rectas distintas y A, B, C tres puntos distintos de r y A’, B’, C’ tres puntos distintos de r’.

Los puntos

U = AB’ ∩ A’B, V = AC’ ∩ A’C, W = BC’ ∩ B’C

están alineados.

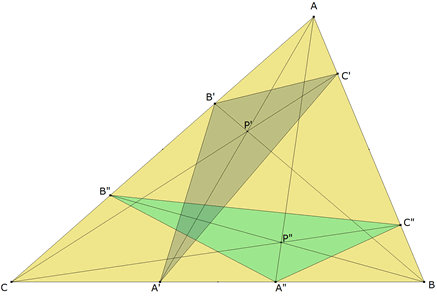
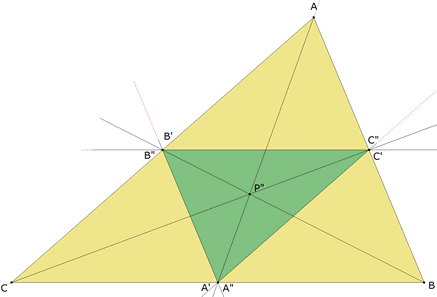
APARTADO (a)

figura 3

Según el enunciado, las cevianas AA’, BB’, CC’ concurren en un punto P’ por lo tanto y por el teorema de Ceva

Según el enunciado también se cumple

Las igualdades anteriores obligan a que

Tenemos entonces que para los puntos A”, B”, C” se cumple

Y aplicando el teorema de Ceva deducimos que las cevianas AA", BB" y CC", concurren en un punto P". (c.q.d.)

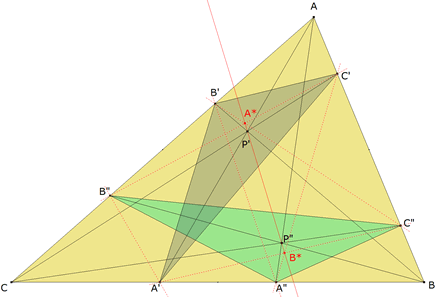
APARTADO (b)

figura 4

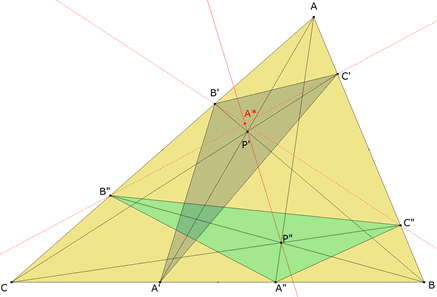
Bastará demostrar la alineación de A* con P’ y P”. El razonamiento para B* y C* sería similar.

Recordando el teorema de Pappus tomamos:

- como primera recta el lado AB y como segunda recta el lado CA

- sobre AB tomamos tres puntos B, C”, C’

- sobre CA tomamos tres puntos C, B”, B’

Se cumple entonces que

Y por el teorema de Pappus A*, P’ y P” están alineados. Del mismo modo demostraríamos la alineación de B* y C*.

APARTADO (c)

figura 5

APARTADO (d)

figura 6

Si P’=G, entonces las cevianas consideradas son medianas que cortarán los lados opuestos en su punto medio y por ello A’=A”, B’=B”, C’=C” y P’=P”=G.

A*, B*, C* no existirían; pues las rectas que les determinan se superponen. No obstante el cociente de razones dobles tiende a 1 a medida que P’ tiende a G y deja de estar definido justo en P’=G.