Problema 243
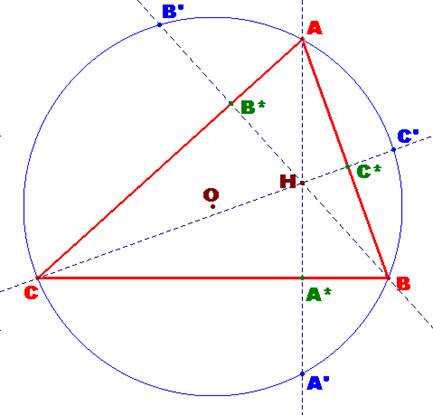
Construir un triángulo conociendo los puntos simétricos del ortocentro respecto a sus tres lados.

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona) Sapiña, J. (1955): Problemas Gráficos de Geometría, Litograf. Madrid.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante, Córdoba (España).

Analizando la figura construida y ya resuelta, destacamos los siguientes hechos de interés:
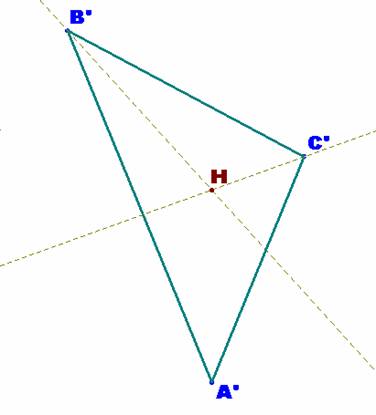
Los puntos A’, B’ y C’, simétricos del ortocentro, H, respecto a sus tres lados, son los transformados por la dilatación (k=2) de centro H de su respectivo triángulo órtico A*B*C*. Como quiera que H es el incentro del triángulo órtico A*B*C*, la construcción de H es obvia a partir del triángulo dado A’B’C’ y, a partir de éste el propio A*B*C*, triángulo órtico del ABC requerido.

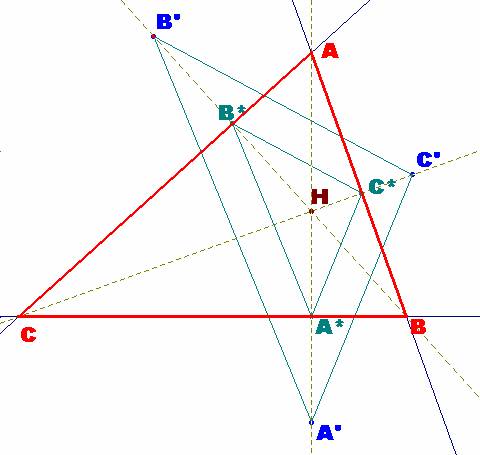
Una vez que tenemos construido el triángulo A*B*C* y el punto H, la construcción del ABC no presenta ninguna dificultad, como se adivina en las siguientes ventanas.