Para el aula (nivel universitario) Problema 243 . Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona) 296 Construir un triángulo conociendo los puntos simétricos del ortocentro respecto a sus tres lados.
(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (16 de mayo de 2005) |
|
Antes de empezar repasaremos tres teoremas BÁSICOS |
TEOREMA I Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición pág. 51 |
|
En una misma circunferencia o en circunferencias iguales, a ángulos centrales iguales corresponden arcos iguales, y a arcos iguales corresponden ángulos centrales iguales. |
|
TEOREMA II Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición pág. 53 |
|
El lugar geométrico de los vértices de todos los ángulos directamente congruentes entre sí cuyos lados pasan por dos puntos fijos A y B, es un arco de circunferencia de extremos A y B, llamado arco capaz del ángulo sobre el segmento AB. |
|
TEOREMA III Pedro Puig Adam. Geometría Métrica, tomo I, 15ª edición pág. 84 |
|
Todo ángulo inscrito en una circunferencia es igual a la mitad del central que comprende el mismo arco. |
|
DISCUSIÓN |
|
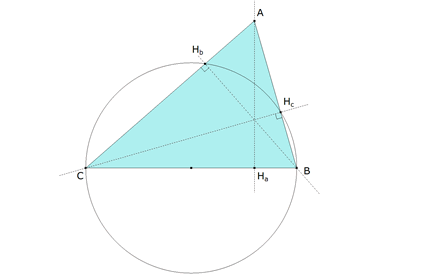
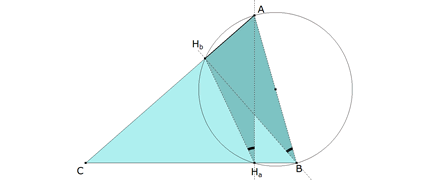
Supongamos que tenemos los pies de las perpendiculares del triángulo ABC
Si el arco es una semicircunferencia el arco central es π y por tanto si consideramos CHbB inscrito en una circunferencia, el valor del ángulo es la mitad del central y Hb=π/2.
Por lo tanto, podemos considerar al triángulo rectángulo como inscrito en un círculo cuyo diámetro es la hipotenusa y el vértice del ángulo recto sobre la circunferencia; y por lo tanto Hc como pie de altura es pie de la perpendicular desde C al lado AB y como tal es el vértice de un ángulo recto y de acuerdo con el párrafo anterior también está sobre la circunferencia de diámetro BC.
|
|
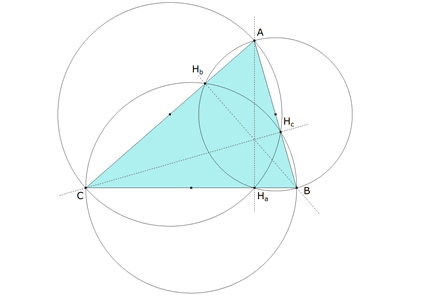
Existen por lo tanto tres círculos que pasan cada uno por dos pies de altura y por los vértices del lado del triángulo al que no pertenecen los pies de altura considerados.
|
|
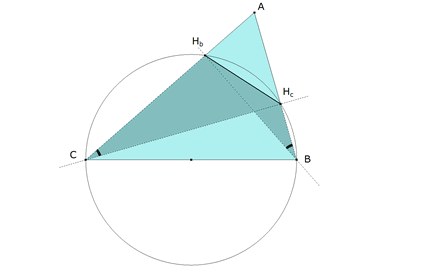
Tomemos ahora, en el círculo HbHcBC, el segmento HbHc; los ángulos HbCHc y HbBHc son iguales y por lo tanto los ángulos ACHc y HbBA, son iguales.
|
|
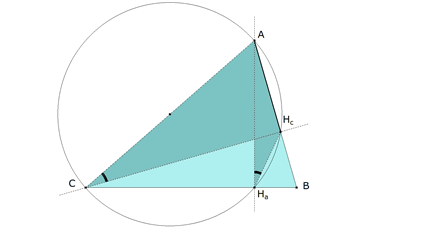
En el círculo HcHaCA consideramos el segmento AHc; los ángulos ACHc y AHaHc son iguales.
|
|
Tomamos el segmento HbA en el círculo HaHbAB; los ángulos HbHaA y HbBA son iguales.
|
|
En la figura 3, los ángulos ACHc y HbBA, son iguales. En la figura 4, los ángulos ACHc y AHaHc son iguales. En la figura 5, los ángulos HbHaA y HbBA son iguales y así
∠HbHaA=∠HbBA=∠ACHc=∠HbBA=∠ACHc=∠AHaHc
∠HbHaA=∠AHaHc
POR LO QUE DEDUCIMOS QUE LA ALTURA AHa ES LA BISECTRIZ DEL ÁNGULO HbHaHc.
|
|
SUPONGAMOS EL PROBLEMA RESUELTO |
|
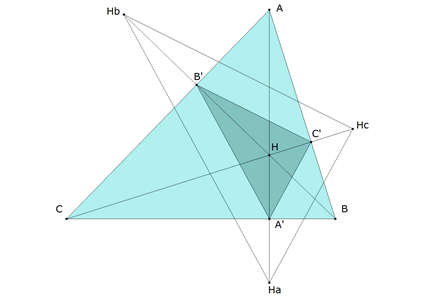
Se ve en la INTRODUCCIÓN que las alturas son las bisectrices del triángulo órtico (triángulo de los pies de las alturas). Veremos ahora que el triángulo HaHbHc formado por los puntos simétricos del ortocentro respecto a los lados del triángulo es homotético al triángulo órtico A’B’C’. Por simetría: HA’ = A’Ha ⇒ HHa = HA’ + A’Ha = 2HA’ ⇒ HHa/HA’ = 2. HB’ = B’Hb ⇒ HHb = HB’ + B’Hb = 2HB’ ⇒ HHb/HB’ = 2. HC’ = C’Hc ⇒ HHc = HC’ + C’Hc = 2HC’ ⇒ HHc/HC’ = 2.
2 = HHa/HA’ = HHb/HB’ = HHc/HC’ =2.
Y por lo tanto los triángulos son homotéticos con centro en H y razón 2.
|
|
SOLUCIÓN |
|
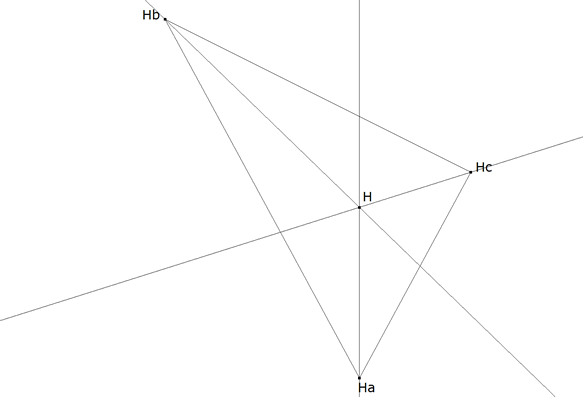
Dado el triángulo HaHbHc podemos hallar H. Intersección de sus bisectrices (INTRODUCCION). Obtenido H podemos hallar los pies de las perpendiculares. (HOMOTECIA INVERSA centro H razón ½) Con los pies de las perpendiculares hallamos los lados del triángulo buscado. (PERPENDICULARIDAD). Con lo anterior tenemos el triángulo buscado. |
|
PASO 1
|
|
PASO 2
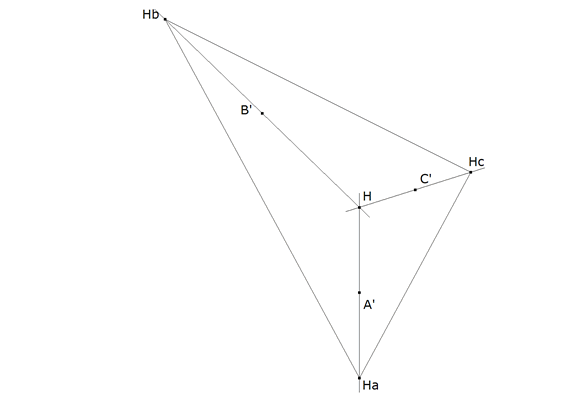 figura 9 figura 9
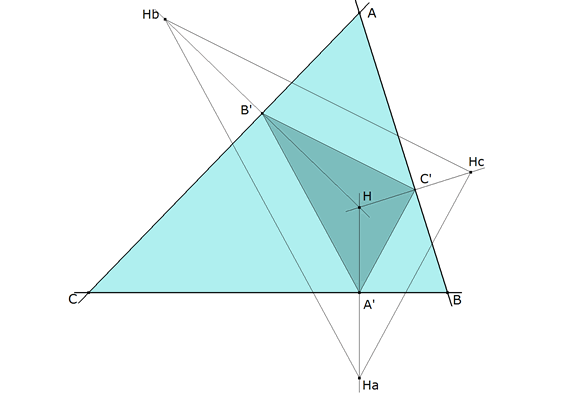
Hallamos los pies de las perpendiculares A’, B’, C’ como puntos medios de HHa, HHb, HHc, respectivamente. O lo que es lo mismo, hallamos el transformado del triángulo HaHbHc por medio de una homotecia de centro H y razón ½.
|
|
PASO 3
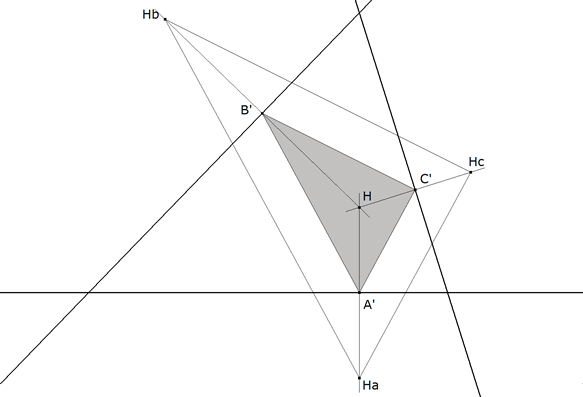 figura 10 figura 10
La perpendicular pA’ por A’ a HA’ contiene al lado BC. La perpendicular pB’ por B’ a HB’ contiene al lado CA. La perpendicular pC’ por C’ a HC’ contiene al lado AB.
|
|
PASO 4
pB’ ∩ pC’= A. pC’ ∩ pA’= B. pA’ ∩ pB’= C.
ABC es el triángulo buscado.
|