Problema 243

Proposat per José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

296 Construïu un triangle coneguent els punts simètrics de l’ortocentre respecte dels seus costats.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solució:

Siguen P, Q, R els punts simètrics de l’ortocentre H del triangle .

Aquests punts pertanyen a les altures del triangle .

P, Q, R són els vèrtexs d’un triangle òrtic que té H ortocentre, aleshores, H és l’incentre del triangle .

Calculem les bisectrius del triangle  la seua intersecció ens donarà el ortocentre del triangle que busquem.

Els costats del triangle que busquem  són les mediatrius dels segments .

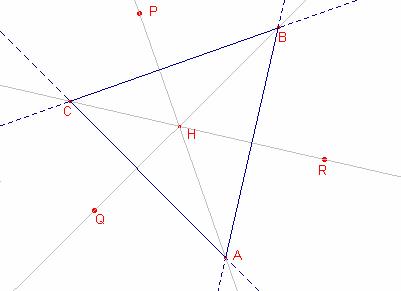
Els problema té 4 solucions si considerem totes les possibilitats de les bisectrius.

Primera solució:

Figura barroso243.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Segona solució:

Figura barroso243b.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Tercera solució:

Figura barroso243c.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Quarta solució:

Figura barroso243d.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava