Problema 243

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

296 Construir un triángulo conociendo los puntos simétricos del ortocentro respecto a sus tres lados.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución:

Sean P, Q, R los puntos simétricos del ortocentre H del triángulo .

Estos puntos pertenecen a las alturas del triángulo .

P, Q, R son los vértices de un triángulo órtico que tiene H ortocentro, entonces, H es el incentro del triángulo .

Calculemos les bisectrices del triángulo  su intersección es el ortocentro del triángulo que buscamos.

Los lados del triángulo que buscamos  son las mediatrices de los segmentos .

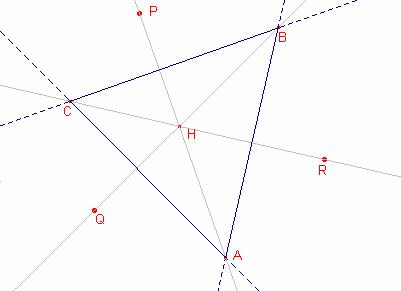
El problema tiene 4 soluciones si consideramos todas les posibilidades de las bisectrices.

Primera solución:

Figura barroso243.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Segunda solución:

Figura barroso243b.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Tercera solución:

Figura barroso243c.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava

Cuarta solución:

Figura barroso243d.fig

Applet created on 16/05/05 by Ricard Peiró with CabriJava