Para el aula (nivel universitario)

Problema 243

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

296 Construir un triángulo conociendo los puntos simétricos del ortocentro respecto a sus tres lados.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid. (Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor )

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca ..- En el problema nº 166 demostramos que los simétricos del ortocentro H de un triángulo ABC respecto de los lados, puntos A”, B”y C”, están en la circunferencia circunscrita al triángulo. Además cada lado es la bisectriz del ángulo con un vértice en el triángulo y los otros dos en un par de simétricos.

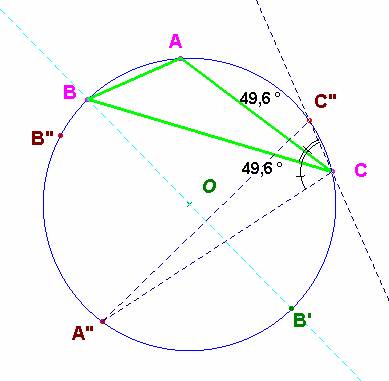
En consecuencia, para construir el triángulo trazamos la circunferencia que pasa por A”, B” y C”. En ella, el lado BC del triángulo buscado es la bisectriz del ángulo C”CA”. Las bisectrices de cualquier ángulo, alcanzan a la mediatriz del lado opuesto en puntos de la circunferencia circunscrita (ver problema nº 8), por ello la mediatriz de A”C” corta en dos puntos a la circunferencia circunscrita: puntos B, B’, candidatos a vértices del triángulo solución. De igual modo las mediatrices de A”B” y B”C” cortan en puntos C y C’, A y A’ respectivamente.

Tomando AC como lado del triángulo solución, el vértice que falta ha de estar en la circunferencia circunscrita y en la perpendicular a ese lado desde B” (paralela a AC’ al ser rectángulo ACC’). De ese modo se encuentra el punto B. H es el ortocentro de este triángulo ABC.

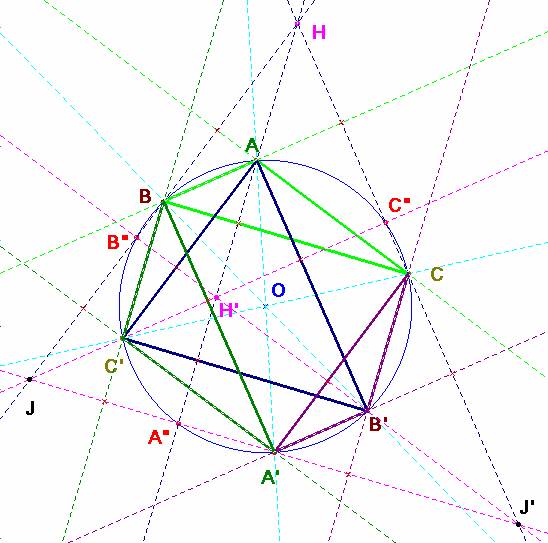
Si en vez de tomar AC elegimos AC’ como lado, el otro vértice se halla en la perpendicular a él desde B” (paralela a AC al ser rectángulo ACC’). Como BB’ es un diámetro, el extremo de esta perpendicular es el punto B’. Obtenemos otra solución, el triángulo AB’C, de ortocentro H’.

Si el punto de partido es el lado A’C o el A’C’, el razonamiento anterior repetido ahora nos da otro par de soluciones en los triángulos A’CB’ y A’C’B, de ortocentros J y J’ respectivamente.

Hay cuatro soluciones que son los triángulos ABC, AB’C, A’CB’ y A’BC’.