Para el aula (nivel universitario)

Problema 243

Propuesto por José María Pedret, ingeniero naval (Esplugues de Llobregat, Barcelona)

296 Construir un triángulo conociendo los puntos simétricos del ortocentro respecto a sus tres lados.

Sapiña, J. (1955): Problemas Gráficos de Geometría,Litograf. Madrid.

(Juan Sapiña Borja, Aparejador, Perito Industrial, Profesor)

Solución

Sabemos que los simétricos del ortocentro respecto de cada uno de sus lados de un triángulo  se encuentran en la circunferencia que inscribe al triángulo.

Luego al unir los puntos simétricos se determina un triángulo A1B1C1 que es semejante al triángulo ortico o pedal a demás de ser homotético con centro de homotecia el ortocentro del triángulo ABC. Luego la bisectriz de los ángulos del triángulo pedal es bisectriz de los formados por los puntos simétricos determinado esta los puntos A, B y C con la circunferencia siendo estos los puntos buscados.

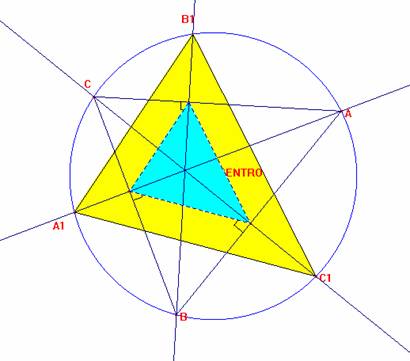
Finalmente para encontrar los vértices de triángulo ABC solo trazamos las bisectrices de los ángulos del triángulo A1B1C1

 

Prof: William Rodríguez Chamache