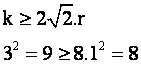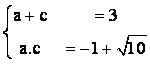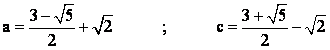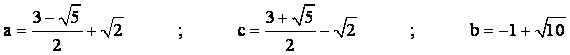Problema 244

Se piden la hipotenusa y los catetos de un triángulo rectángulo conocidas la suma k de los catetos y la altura r correspondiente a la hipotenusa.

Discusión completa del problema y aplicación de las fórmulas obtenidas para el caso k=3 y r=1 Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

MATEMATICA ELEMENTAL (1948)
Revista publicada por el instituto Jorge Juan de Matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº5 EJERCICIOS PROPUESTOS por Escuela Especial de Ingenieros de Montes.

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante, Córdoba (España).

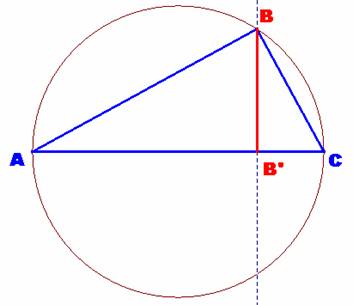
Analizando los datos dados, resulta que:
Como a² + c² = b² y [ABC] =1/2∙a∙c =1/2∙b∙r

entonces a∙c = b∙r

Por tanto: (a+c)² = a² + c² + 2∙a∙c = k² ; b² + 2∙a∙c = k² ; b² + 2∙b∙r = k² ;

Luego entonces será b² + 2∙b∙r − k² = 0, cuya solución positiva no presenta ninguna dificultad:

Para este valor de b (hipotenusa), obtendríamos que los catetos del triángulo, a y c, verificarían las siguientes ecuaciones:

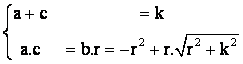o, equivalentemente, la siguiente ecuación de segundo grado: cuyas soluciones dependerán del signo de su discriminante. Por tanto, el problema tendrá solución sii D³ 0.

En definitiva,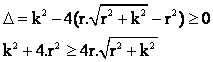

Como quiera que ambas expresiones son positivas, la desigualdad anterior será equivalente a esta otra: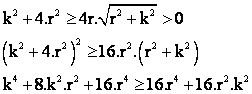

Es decir,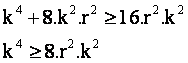

Por lo tanto,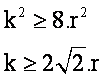

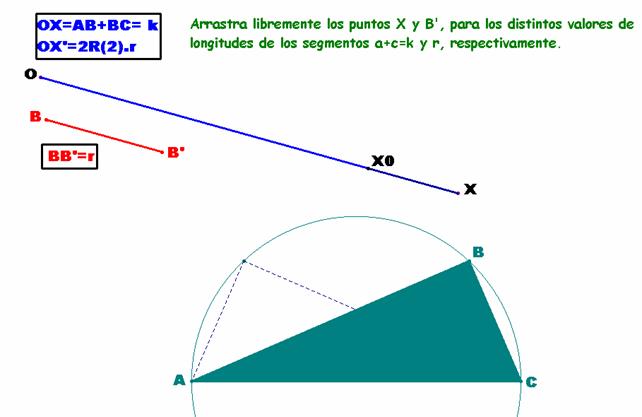
Construyamos a continuación la solución de un modo geométrico, dados las longitudes k y r.

Caso Particular:

k=3; r=1.
En este caso, se cumple que:

Luego los lados del triángulo rectángulo son: