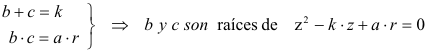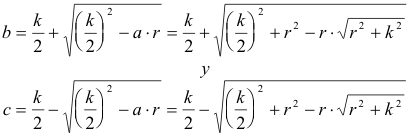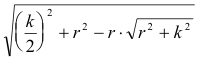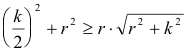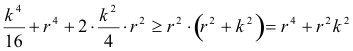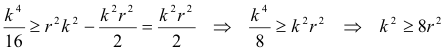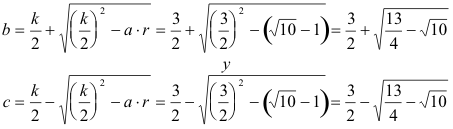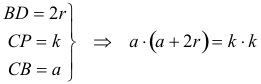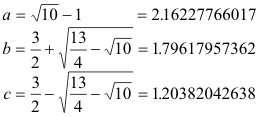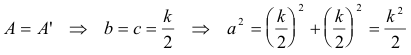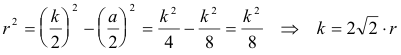Problema 244. Propuesto por Maite Peña Alcaraz, estudiante de Industriales en la Universidad de Comillas (Madrid).

704. Se piden la hipotenusa y los catetos de un triángulo rectángulo conocidas la suma k de los catetos y la altura r correspondiente a la hipotenusa.

Discusión completa del problema y aplicación de las fórmulas obtenidas para el caso k=3 y r=1.

MATEMATICA ELEMENTAL (1948) Revista publicada por el instituto Jorge Juan de matemáticas y la Real Sociedad Matemática Española 4ª Serie – Tomo VIII nº5 EJERCICIOS PROPUESTOS por Escuela Especial de Ingenieros de Montes.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (17 de mayo de 2005)

PLANTEAMIENTO

figura 1

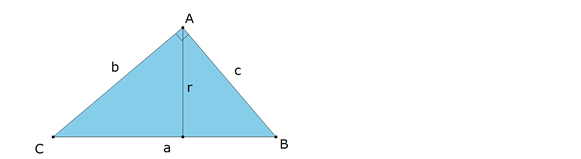
Según el enunciado, se conocen

Si expresamos el área del triángulo, tenemos

Elevando k al cuadrado, tenemos

Con la relación anterior podemos obtener a tanto algebraica como gráficamente.

Obtenida la hipotenusa a, sabemos que

Por lo tanto

DISCUSION

Para que haya solución debe existir

Y por lo tanto debe ser

que elevando al cuadrado miembro a miembro queda

que nos proporciona la condición

y extrayendo la raíz cuadrada

RESOLUCION NUMERICA

Si k=3 y r =1

y entonces

RESOLUCION GRAFICA

Sorprendentemente la resolución gráfica es muchísimo más sencilla ya que sólo se trata de resolver la ecuación que nos proporciona el valor de la hipotenusa a. Luego es muy fácil obtener un triángulo rectángulo de hipotenusa a y altura r; sin tener que preocuparnos de b y c que aparecerán automáticamente.

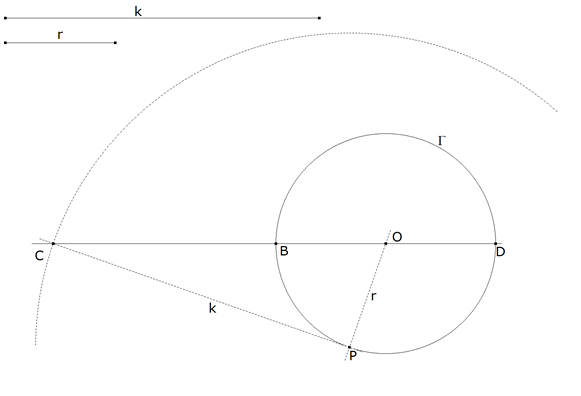
PASO 1. OBTENCION DE LA HIPOTENUSA a.

figura 2

Dados k y r; con centro en un punto cualquiera O trazamos el círculo Γ de centro O y radio OP=r.

Con centro en P trazamos un arco de radio PC=k.

Trazamos la recta por CO que corta a Γ en B y D.

BC ES LA HIPOTENUSA a DEL TRIÁNGULO BUSCADO.

En efecto, recordando la potencia de un punto respecto a un círculo Γ y particularizando para C

y entonces

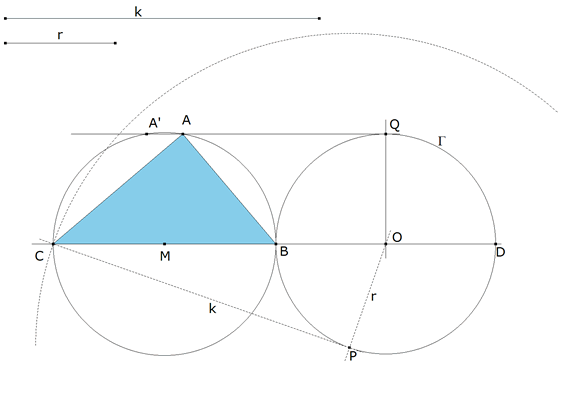
PASO 2. OBTENCION DEL VERTICE A.

figura 3

Calculado BC, tomamos M punto medio de BC.

Con centro en M trazamos el círculo de diámetro BC.

Por O trazamos una perpendicular a BC que corta a Γ en Q.

Por Q una paralela a BC que corta al círculo de diámetro BC en A y A’.

ABC ES EL TRIANGULO BUSCADO.

En efecto

y por tanto ABC es el triángulo rectángulo de hipotenusa a obtenida a partir de k y r con altura r.

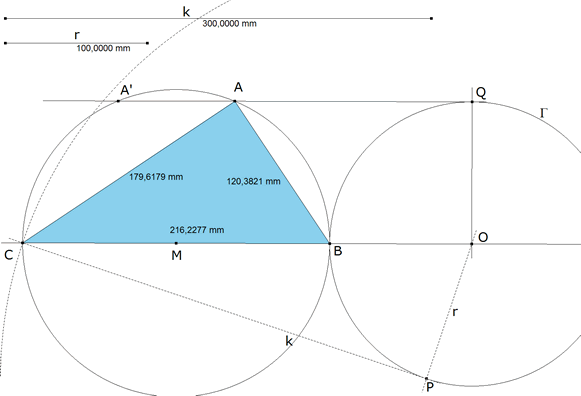
COMPROBACION CON CABRI II Plus

figura 4

En CABRI II Plus para k=300mm y r =100mm obtenemos

Vemos que el caso límite sería cuando QA fuera tangente al círculo de diámetro BC; entonces A=A’ y el triángulo sería isósceles con b=c.

y de aquí para el triángulo mitad