Problema 245:

Sea P un punto interior del triángulo ABC, siendo A₁B₁C₁ su triángulo ceviano. Si trazamos un círculo tangente a BC por A₁ y al circuncírculo (O) de ABC, determinamos el punto de tangencia A₂ situado en el arco que no contiene a A. De manera similar definimos los puntos B₂, C₂.

A) Probar que AA₂, BB₂, CC₂ son concurrentes.

Salazar, J.C. (2005): Propuesta personal.

B) Si P es el punto de Gergonne, A₂A₁, B₂B₁ y C₂C₁ son concurrentes.

Taller de Olimpiadas de Vietnam (2005).

Solución de Juan Carlos Salazar,profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz) :

A) Tenemos que A₂A₁, B₂B₁, C₂C₁ son bisectrices de <BA₂C, <CB₂A, <AC₂B respectivamente.

Probaremos que A₂A₁ es bisectriz de <BA₂C: trazamos una tangente por A₂ que corta a BC en el punto F (Ver Fig. 1):

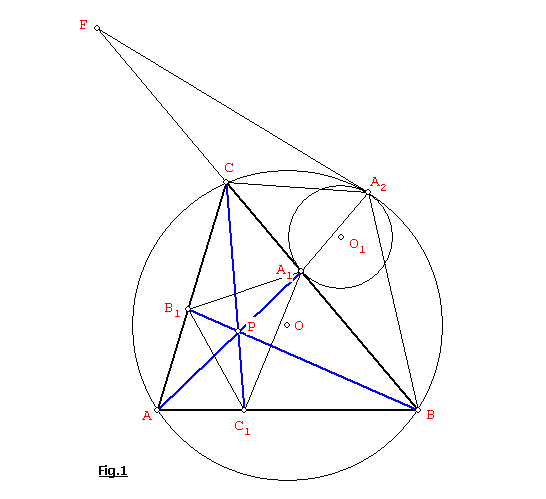
Luego FA₁A₂ es isósceles, ya que FA₁ = FA₂, también <CA₂F = <A₂BC.

También: <A₁A₂F = <A₁A₂C + <CA₂F = <FA₁A₂ = <A₁A₂B + <A₁BA₂ =

<A₁A₂B + <CBA₂ = <A₁A₂B + <CA₂F

Entonces <A₁A₂C = <A₁A₂B, o sea que A₂A₁ es bisectriz de <BA₂C.

De manera similar podemos probar que B₂B₁, C₂C₁ son bisectrices de <CB₂A, <AC₂B respectivamente. No está demás puntualizar que las bisectrices A₂A₁, B₂B₁, C₂C₁ se encuentran con las mediatrices de los lados BC, CA, AB en puntos del cicuncírculo (O).

Considerando el triángulo ceviano ABC₁ del punto P, aplicamos el teorema de la bisectriz, en los triángulos BA₂C, CB₂A, AC₂B (Ver Fig. 2):

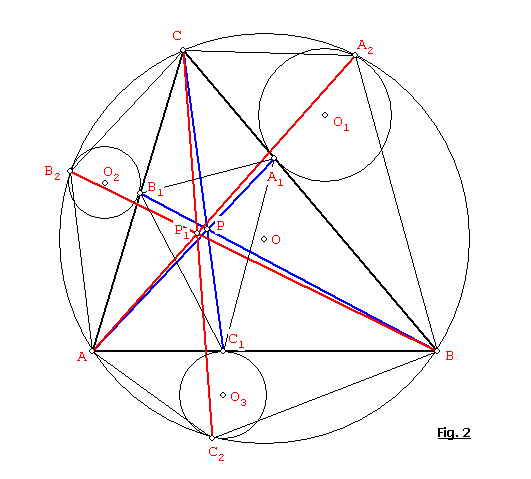
CA₂/BA₂ = CA₁/BA₁

AB₂/CB₂ = AB₁/CB₁

BC₂/AC₂ = BC₁/AC₁

Por lo tanto:

(CA₂/BA₂).(AB₂/CB₂).(BC₂/AC₂) = (CA₁/BA₁).(AB₁/CB₁).(BC₁/AC₁)

Como: (CA₁/BA₁).(AB₁/CB₁).(BC₁/AC₁) = 1, por aplicación del teorema de Ceva en el triángulo ABC, donde AA₁, BB₁, CC₁ concurren en P.

Luego: AB₂.BC₂.CA₂ = AC₂.BA₂.CB₂

Esta última relación nos indica que se cumple el teorema de Ceva aplicado al círculo (O), entonces AA₂, BB₂, CC₂ concurren en un punto P₁. QED.

B) Cuando P es el punto de Gergonne, los vértices A₁, B₁, C₁ de su triángulo ceviano son los puntos de tangencia de los círculos (O₁), (O₂), (O₃) con el incírculo (I) de ABC. (Ver Fig. 3).

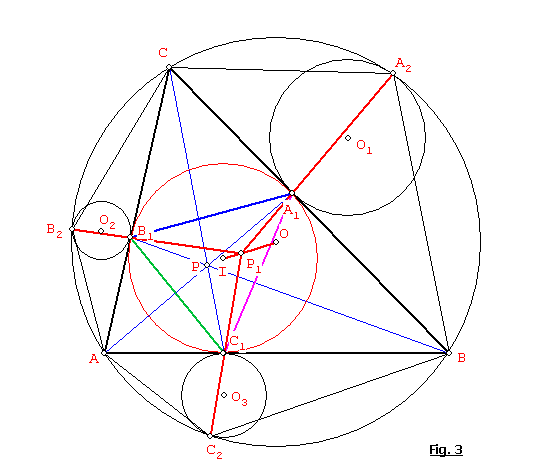
Por lo tanto A₁ es el centro de similitud interna del círculo (O₁) e incírculo (I), también A₂ es el centro de similitud externa de los círculos (O₁) y (O). Si aplicamos el Teorema de Monge, la recta A₂A₁ debe pasar por el centro de similitud interna P₁ del circuncírculo (O) e incírculo (I), que es colineal con los centros O e I. De manera análoga las rectas B₂B₁, C₂C₁ deben de pasar por el centro de similitud interna P₁de los círculos (O) e (I), es decir que las rectas A₂A₁, B₂B₁, C₂C₁ concurren en P₁.

Es conveniente mencionar que además se cumple, sin considerar segmentos orientados:

IP₁/P₁O= r/R, donde r y R son el inradio y circunradio del triángulo ABC. QED.

Desde otro punto de vista, si consideramos que A₂A₁ se intersecta con la mediatriz de BC en el punto A₃ sobre el circuncírculo (O), que es punto medio del arco BAC, luego AA₃ es bisectriz exterior del <A, y por lo tanto AA₃ es paralela al lado B₁C₁ del triangulo formado por los puntos de tangencia del incírculo (I) con el triángulo ABC. Análogamente si consideramos los puntos B3, C3 que son puntos medios de los arcos ABC y BCA, también tenemos que BB₃//A₁C₁ y CC₃//A₁B₁. (Ver Fig.4)

Podemos concluir además que el triángulo A₃B₃C₃ es el triángulo mediano del triángulo excentral de ABC, igualmente también se cumple que los triángulos A₃B₃C₃ y A₁B₁C₁ son homotéticos porque sus lados son respectivamente paralelos. Por lo tanto el centro de homotecia (P₁) es colineal con los centros del circuncírculo (O) e incírculo (I), o sea que A₂A₁ (A₃A₁) , B₂B₁ (B₃B₁), C₂C₁ (C₃C₁) pasan por el centro de homotecia P₁, donde además la razón de homotecia es igual a la relación entre sus circunradios, es decir: P₁I /P₁O= r/R. QED.