Problema 246

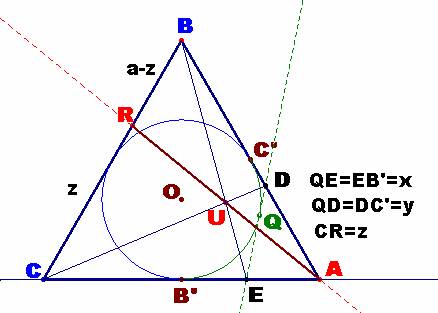
Sea ABC un triángulo equilátero y Q su circunferencia inscrita. Sean D y E puntos de los lados AB  y AC, respectivamente, tales que DE es tangente a Q por el arco más cercano a A. La intersección de BE y CD es U; se prolonga AU hasta cortar a BC en R.

Demostrar que U es punto medio de AR.

Ramos L. (2005): Comunicación personal.

Solución de F. Damián Aranda Ballesteros, profesor de Matemáticas del IES Blas Infante, Córdoba (España).

* Sean los segmentos:
QE=EB’=x
QD=DC’=y
CR=z
AB=BC=CA=a

donde B’ y C’ son los puntos medios de los lados AC y AB, respectivamente.
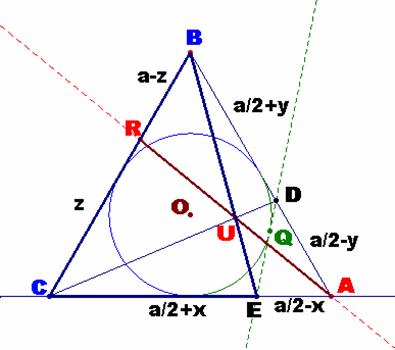
Como las cevianas AR, BE y CD se cortan en el punto U, tenemos que se verifica la siguiente relación: .

De esta relación deducimos la expresión de z en función de x e y.

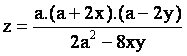
En el triángulo AED, tenemos por el teorema de los cosenos que:

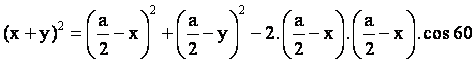
de donde deducimos la siguiente relación:

que nos permite expresar y en función de x:

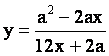
y así expresar z como:

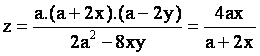
· Considerando ahora el triángulo BCE, y la recta que pasa por los puntos A, U y R , tenemos por el Teorema de Menelao que:
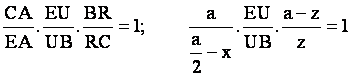
y así: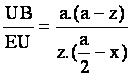
Por otra parte, teniendo en cuenta la razón de alturas de los puntos U y B hasta el lado AC, es decir h_U y h_B,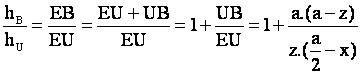
Como 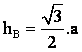, entonces: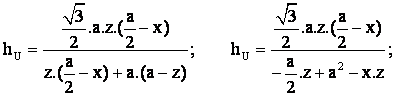

· Buscamos la expresión de h_R , la altura del punto R hasta el lado AC.
Si [ACR]=Área del triángulo ACR, tenemos que

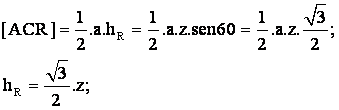
· Por fin, cuál es la razón entre las alturas h_R y h_U.

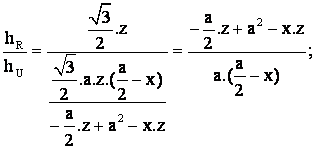
Sustituyendo ahora por la expresión de z, antes obtenida,

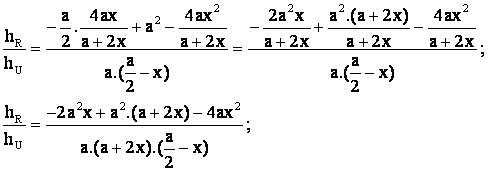
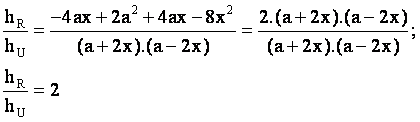
· Esta última razón prueba que el punto U es el punto medio de AR.