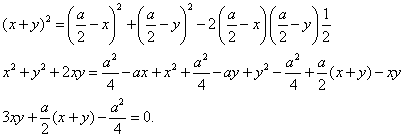Sean M y N los puntos
medios de los lados AB y AC, respectivamente. Al ser MN paralela a BC, que U
sea el punto medio de AR equivale a decir que U está pertenece al segmento
MN. Así que...
Problema 246 de triánguloscabri |
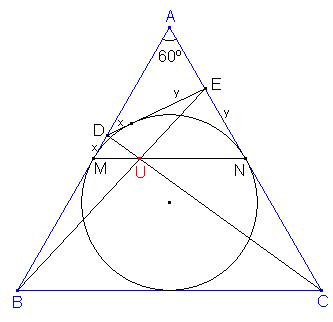
| Sea ABC un triángulo equilatero y Q su circunferencia inscrita. Sean D y E puntos de los lados AB y AC, respectivamente, tales que DE es tangente a Q por el arco más cercano a A. La intersección de BE y CD es U; se prolonga AU hasta cortar a BC en R. Demostrar que U es punto medio de AR. |
|
Propuesto por Luis Ramos Castilla. |
Solución de Francisco Javier García Capitán
Sean M y N los puntos
medios de los lados AB y AC, respectivamente. Al ser MN paralela a BC, que U
sea el punto medio de AR equivale a decir que U está pertenece al segmento
MN. Así que...
... supongamos el problema resuelto:
Que U está en MN equivale a decir que U es el centro de una proyección de la recta AB sobre la recta AC en la que A, B, D, M se proyectan sobre A, E, C, N. Como las proyecciones, caso particular de las proyectividades, conservan las razones dobles, será
(ABDM) = (AECN)
Entonces
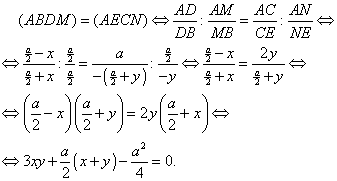
El problema estará resuelto si comprobamos que las longitudes x e y cumplen esta última igualdad.
Pero ello es inmediato si aplicamos el teorema del coseno al triángulo ADE:
