Propuesto por Luis Ramos Castilla (Lima, Perú)

Problema 246

Sea ABC un triángulo equilátero y Q su circunferencia inscrita. Sean D y E puntos de los lados AB y AC, respectivamente, tales que DE es tangente a Q por el arco más cercano a A. La intersección de BE y CD es U; se prolonga AU hasta cortar a BC en R. Demostrar que U es punto medio de AR.

Ramos L. (2005): Comunicación personal.

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). (1 de junio de 2005)

PLANTEAMIENTO

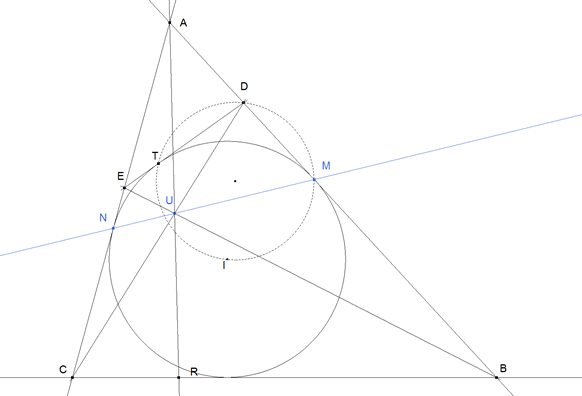
figura 1

Vamos a demostrar que, en un triángulo cualquiera, el lugar geométrico del punto U es una recta que pasa por los puntos de contacto M y N del círculo inscrito con los lados AB y AC.

Gracias a las simetrías del triángulo equilátero, los puntos de contacto, están en el punto medio de los lados. La recta que contiene a U será paralela a BC y por tanto U estará en el punto medio de AR.

TEOREMAS

TEOREMA UNO

Dada una cónica, los puntos de intersección de una tangente móvil con dos tangentes fijas son homográficos.

Podemos ver este teorema y otros con su demostración en el teorema 4.1 del problema 182 de las páginas de RICARDO BARROSO CAMPOS:

http://www.aloj.us.es/rbarroso/trianguloscabri/sol/sol182ped.htm

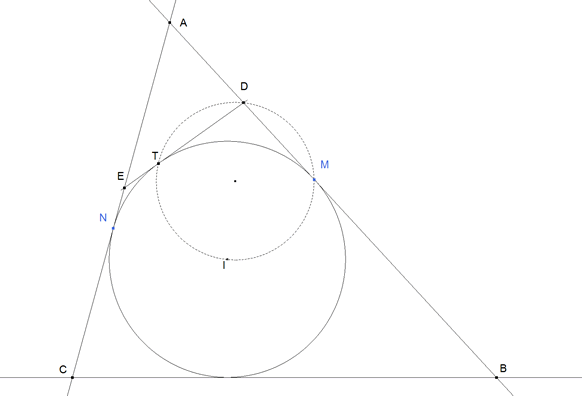
figura 2

Traducido a nuestro problema, la cónica es el círculo inscrito, la tangente móvil es ED, la primera tangente fija es AB y la segunda tangente fija es AC.

Por lo tanto existe una homografía h

Es claro que en esta homografía

Tomando ahora B* y C*, dos haces de rectas por B y C respectivamente definimos la siguiente biyección h*

Al ser D y E homográficos, podemos afirmar que las rectas BE y CD también lo son y por lo tanto

h* ES UNA HOMOGRAFÍA DE HACES DE RECTAS

TEOREMA DOS

Cuando dos haces de cuatro rectas son homográficos, si una de las rectas coincide con su imagen, las tres rectas restantes del haz cortan a sus rectas correspondientes en el otro haz en tres puntos situados en línea recta.

Podemos ver este teorema y otros con su demostración en el teorema 2.1 del problema 200 (Gergonne y el problema de Castillon) de las páginas de RICARDO BARROSO CAMPOS:

http://www.aloj.us.es/rbarroso/trianguloscabri/200extraped/gergonne.htm

Este enunciado no significa más que la homografía es una proyección entre haces de rectas. Cosa que ocurre en nuestro caso ya que

En este problema

Y esa recta es MN ya que hemos visto que

CONCLUSION

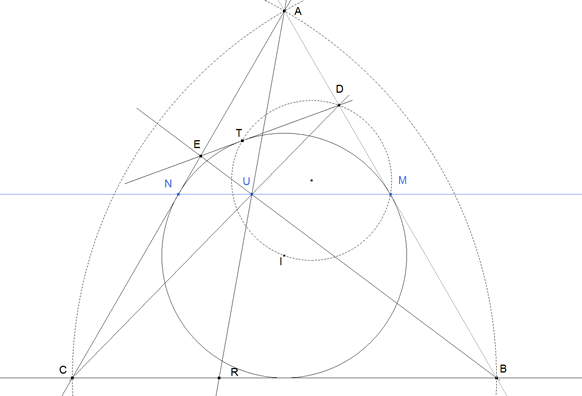
figura 3

En el caso de que ABC sea equilátero, M y N son los puntos medios respectivos de AB y AC y como U pertenece a MN y R pertenece a BC

Y en consecuencia U es el punto medio de AR.