Teorema de Menelau.

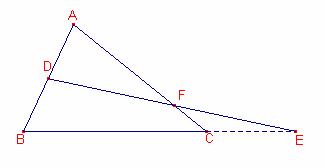
Siga el triangle , siguen els punts .

Siga la recta g que passa pels punts B, C. Siga el punt .

D, E, F estan alineats Û

Problema 246

Propuesto por Luis Ramos Castilla (Lima, Perú)

Siga un triangle equilàter i Q la seua circumferència inscrita.

Siguen D i E punts dels costats , , respectivament, tal que és tangent a la circumferència Q per l’arc més a prop a A.

La intersecció de i és U.

Es prolonga fins tallar el costat en R.

Demostreu que U és el punt mig de .

Ramos L. (2005): Comunicación personal.

Solució:

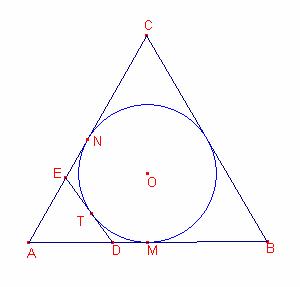
Siga un triangle equilàter .

Siga tangent a la circumferència Q inscrita del triangle. Siga T el punt de tangència del segment i la circumferència Q.

Siguen M, N punts de tangència de la circumferència inscrita i el triangle

.

,

.

Aleshores el perímetre del triangle és:

.

Siga , , Aleshores, .

Aplicant el teorema del cosinus al triangle :

.

. Simplificant:

(1)

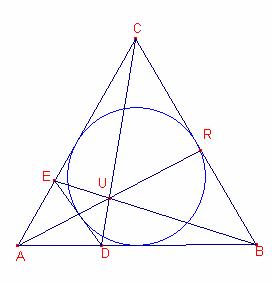
Aplicant el teorema de Menelau al triangle :

. Aleshores, (2)

Aplicant el teorema de Menelau al triangle :

. Aleshores, (3)

Sumant les expressions (2) (3):

.

(4)

Substituint l’expressió (1) en el denominador de l’expressió (4):

.

Aleshores, , per tant U és el punt mig del segment .